Pose purposeful questions: Effective teaching of mathematics uses purposeful questions to assess and advance students’ reasoning and sense making about important mathematical ideas and relationships.
- NCTM 2014, p. 35
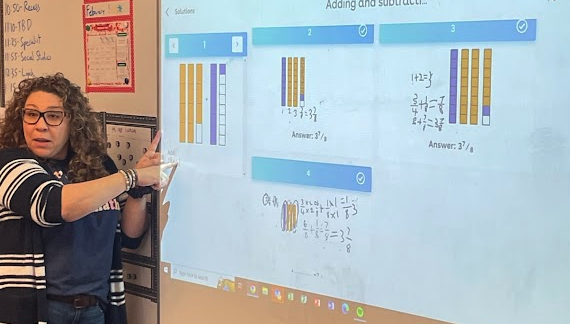
In this picture, my colleague Monique is facilitating a conversation with a class centered around specific student solutions. The questions we ask and how we ask them are often key to how successfully our students make connections, deepen their reasoning, and learn from and with each other. And possibly even more interesting to consider are the questions our students ask and how to use their questions to create a vibrant democratic learning environment.
One of the features of Principles to Action that I find especially helpful are the tables they include for each of the math teaching practices. These tables list teacher and student actions for each practice. Here is the table for the practice of posing purposeful practices.
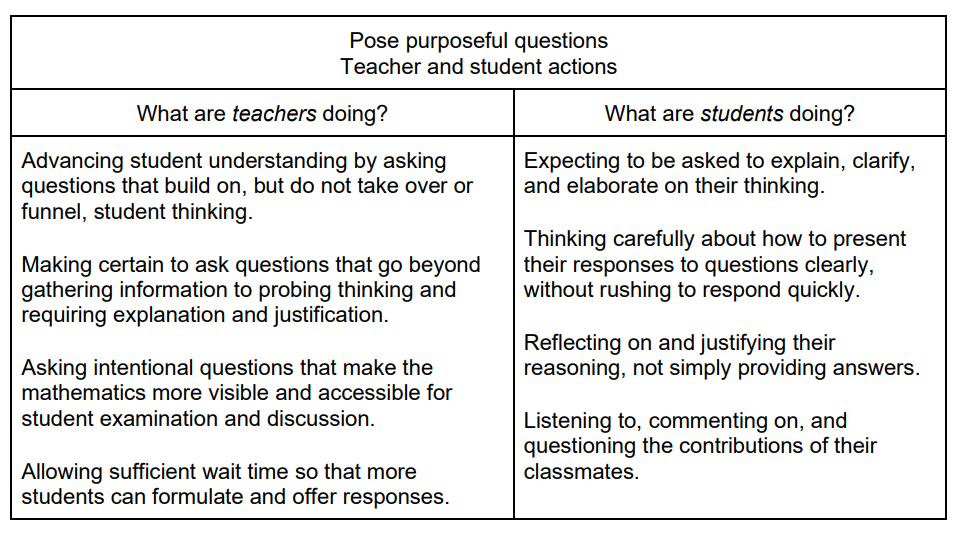
When I was a new teacher, I tended to ask lots of questions like What’s the y-intercept in the graph? What's the rise? What’s the run? So, what’s the slope? I knew questions were important, but I hadn’t learned that there are different types of questions that we teachers ask. The questions I asked as an early career teacher were all focused on gathering information and funneling students as I led them to the conclusion I had in mind. I knew where I wanted the lesson to go, and as I asked questions, I probably responded more positively to student answers that were on the path I had planned while limiting my attention to responses that took a different route. Now, I try to ask questions that are exemplified by the left side of the table so that my students will be doing the actions on the right.
In the last several decades, math education researchers have developed frameworks to categorize the types of questions that teachers ask, and these categories can help us improve the types of questions that we use and how we use them. One framework categorizes questions into four types:
- Gathering information
- Probing thinking
- Making the mathematics visible
- Encouraging reflection and justification
The other framework attends to how we use questions and identifies two patterns called funneling and focusing. Funneling involves using a set of questions to get students to a desired procedure or conclusion. Focusing, on the other hand, involves the teacher paying attention to what the students are thinking, pressing them to communicate their thoughts clearly, and expecting them to reflect on their thoughts and those of their classmates” (Principles to Action, p. 37). There is a wonderful article called Questioning our Patterns of Questioning (2005) by Herbel-Eisenmann and Breyfogle that hugely impacted my practice.
Learning to use focusing questions and vary the types of questions we ask takes time, practice, and intentional planning. We can use the student solution view in Magma Math to help us as we examine our students’ work and plan what types of questions to ask as we move students toward the mathematical goals for the unit of study.
Let’s consider a lesson in which a teacher is using Magma. The goal for the lesson (and unit) is for students to use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem (CCSS 3.OA.A.3).
Here is a problem that was assigned to the students, with a sampling of their solutions below it. Imagine the students worked on the problem towards the end of the lesson today, and I want to use students’ work as a basis for launching the lesson tomorrow. (I’m giving myself time to look over student solutions and make decisions as I plan.)

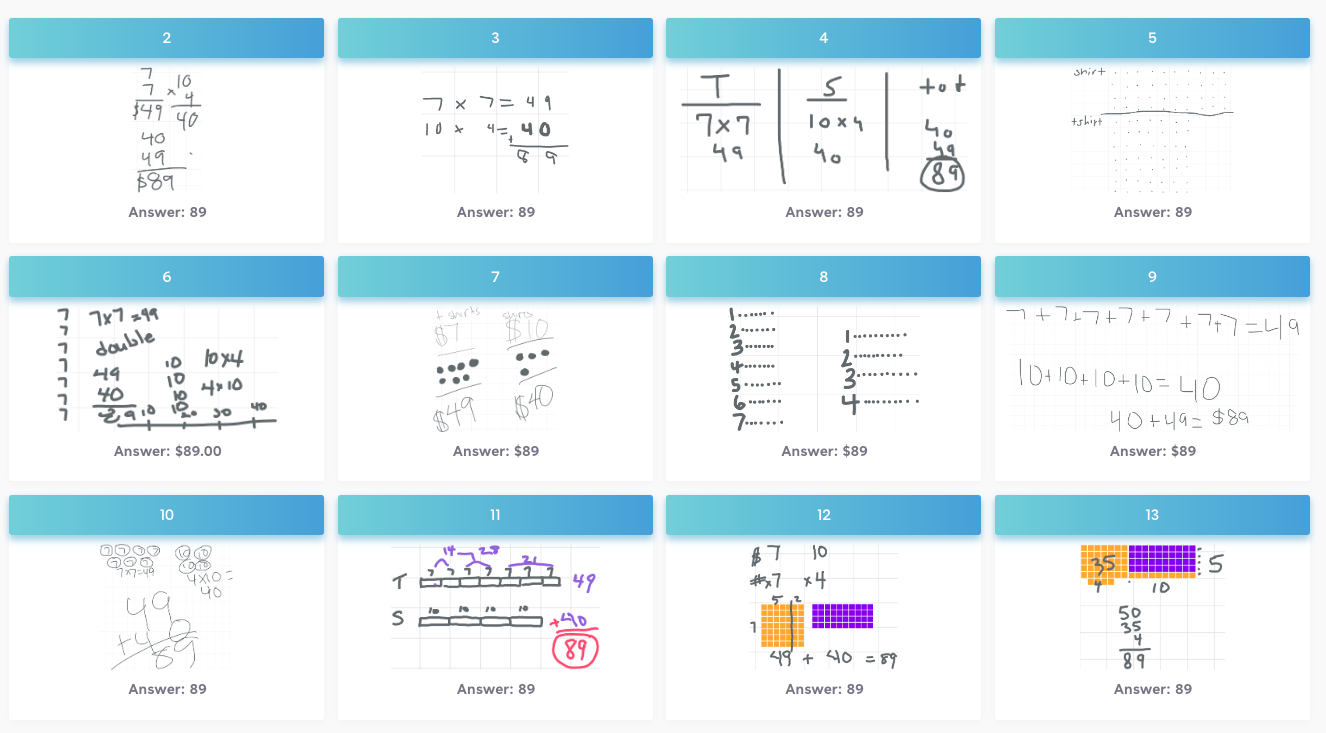
As I look across these solutions, I am thinking about what questions I want to ask my students. How can I attend to what they are thinking, help them communicate their thoughts clearly, and to reflect on their thoughts as well as the ideas their classmates have shared?
As I plan my questions, I also want to think about the sequence of how I’ll share solutions. I would be inclined to begin with the student solutions that are more concrete - For example students #5, 8, 11 and 12.
Best,
Leslie
leslie@magmamath.com



%20(1).jpg)

%20(1).png)


