Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems.

-NCTM (2014), p. 42

When I was an elementary math student, and even well into middle school, I couldn’t remember the answer to many math facts quickly, and 7 x 8 was the worst. I remember flash cards, and games where I would fail for my team or have to go sit down when I got it wrong. My dad quizzed me at dinner in an attempt to help me remember, but nothing helped. Sometimes he would kindly explain that I should think about 7 x 7 and then add another 7, or think about 8 x 8 and subtract an 8, but none of those explanations helped me. It seemed I was doomed to be a failure in math!

‍I didn’t really develop fluency with some math facts until I started working with elementary math students and teachers and explored ways to build conceptual understanding of math. Once I started seeing that 7 x 7 could be represented as area or as groups of things, understanding of my father’s explanations started making sense!

For example, here are 7 rows of 8 tiles, as well as 8 rows of 7 tiles (a convincing argument that 7 X 8 = 8 x 7!)

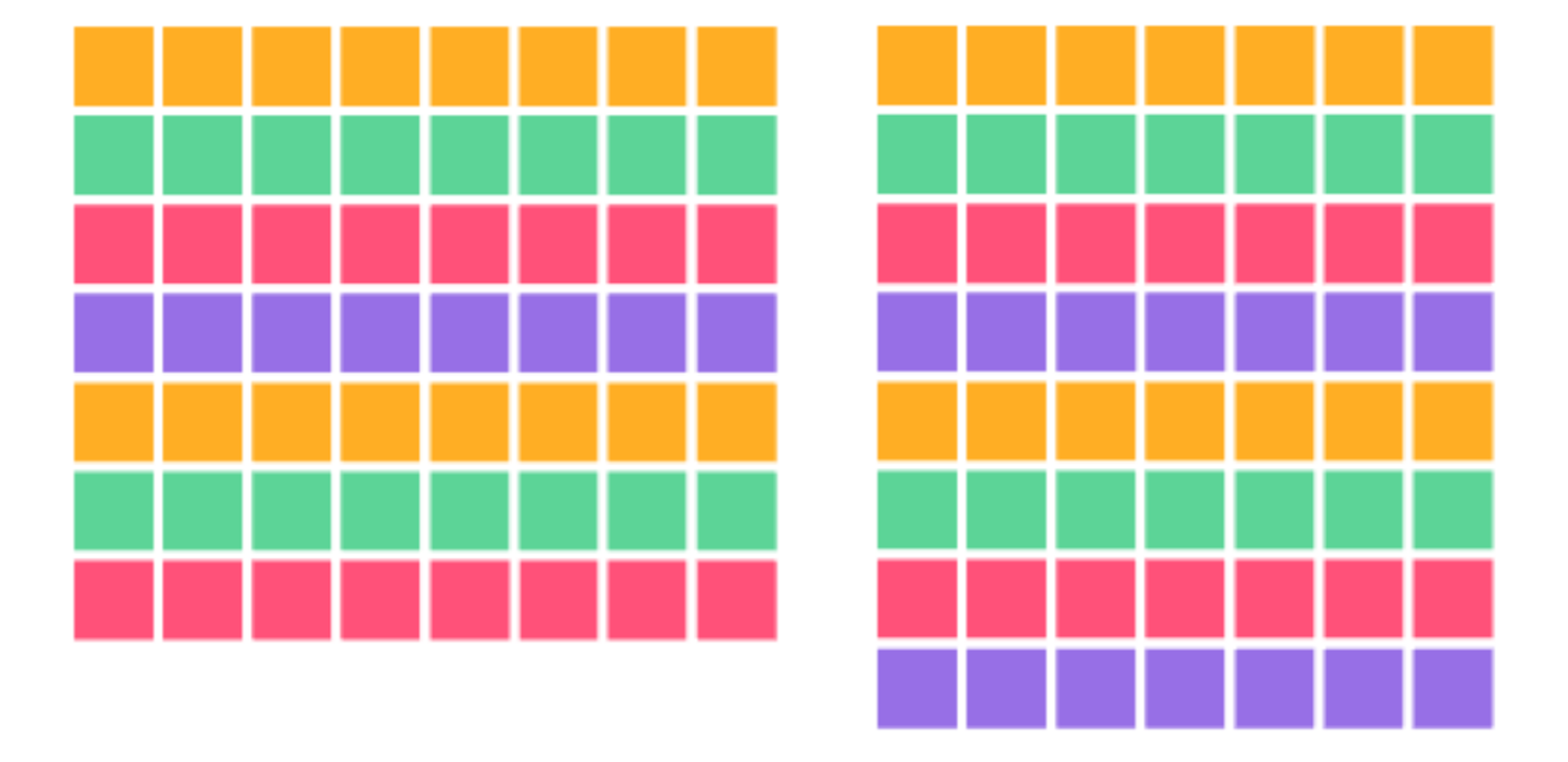
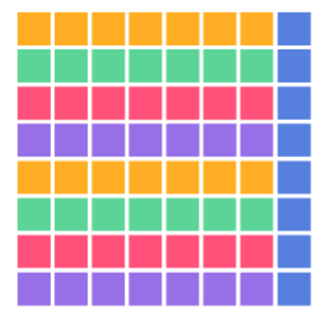
If we had gotten out tiles or chips or something (sugar cubes? buttons?) to build these arrays some of the explanations would have made much more sense to me. Now I can see what’s happening as if I start with 8 x 8 and then take away one of the 8’s, it helps me build a conceptual understanding of what 7 x 8 means.

Or, I could start with 7 groups of 7 tiles, and then add one more group of 7 tiles, thinking about 7 x 8 as 7 x 7 + 7 = 49 + 7 = 56!

But as my thinking has evolved, my favorite way to quickly confirm for myself what 7 x 8 became is thinking about it as 8 x 7, and thinking about multiplying by 8 as doubling three times.

So I have 2 x 7 = 14

then 2 x 14 = 28

and lastly 2 x 28 = 56!

Double, double, double!!!
‍

As learners have the opportunity to play creatively with mathematics - via manipulatives, number talks, Magma Math and/or discussions, they develop conceptual understanding which becomes the foundation for procedural fluency. In one of our recent Magma Onboarding Professional Learning sessions with elementary math teachers, we had a wonderful conversation that highlighted how fluency builds out of conceptual understanding. Consider the distributive property: a(b + c) = ab + ac. In the session, we discussed this problem:

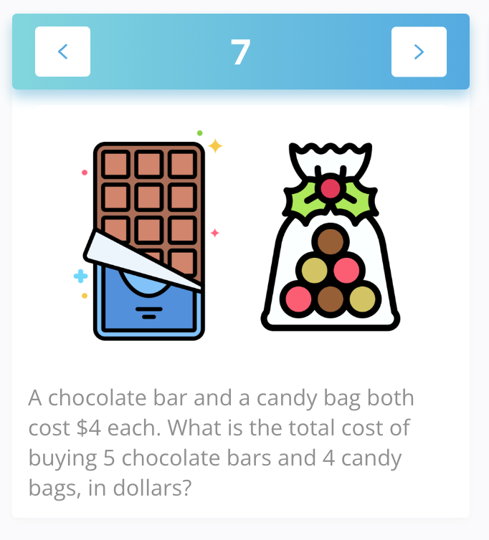
Take a few minutes and think about how you would solve it. How might your students solve it?
Then we used a routine called Same But Different to explore the two student solutions below. Look at the two solutions, and consider, how are they the same? And how are they different?

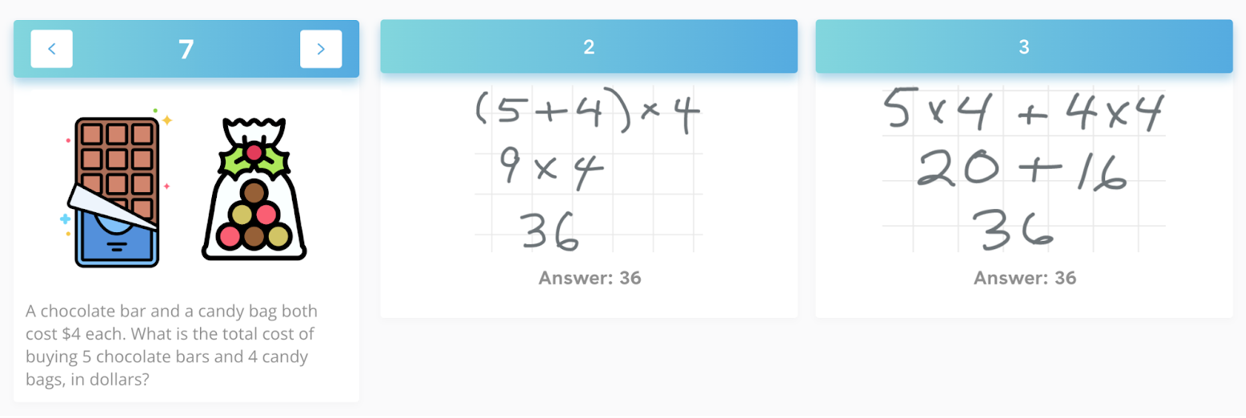
As a group, we generated a chart like this one, listing the ways the solutions are the same, and how they are different. As we did this, when participants shared, they always started by restating what someone before them had said, and then either added on or started a new thread. I also asked them to use the sentence stems, “They are the same because…….” or “They are different because….”
‍

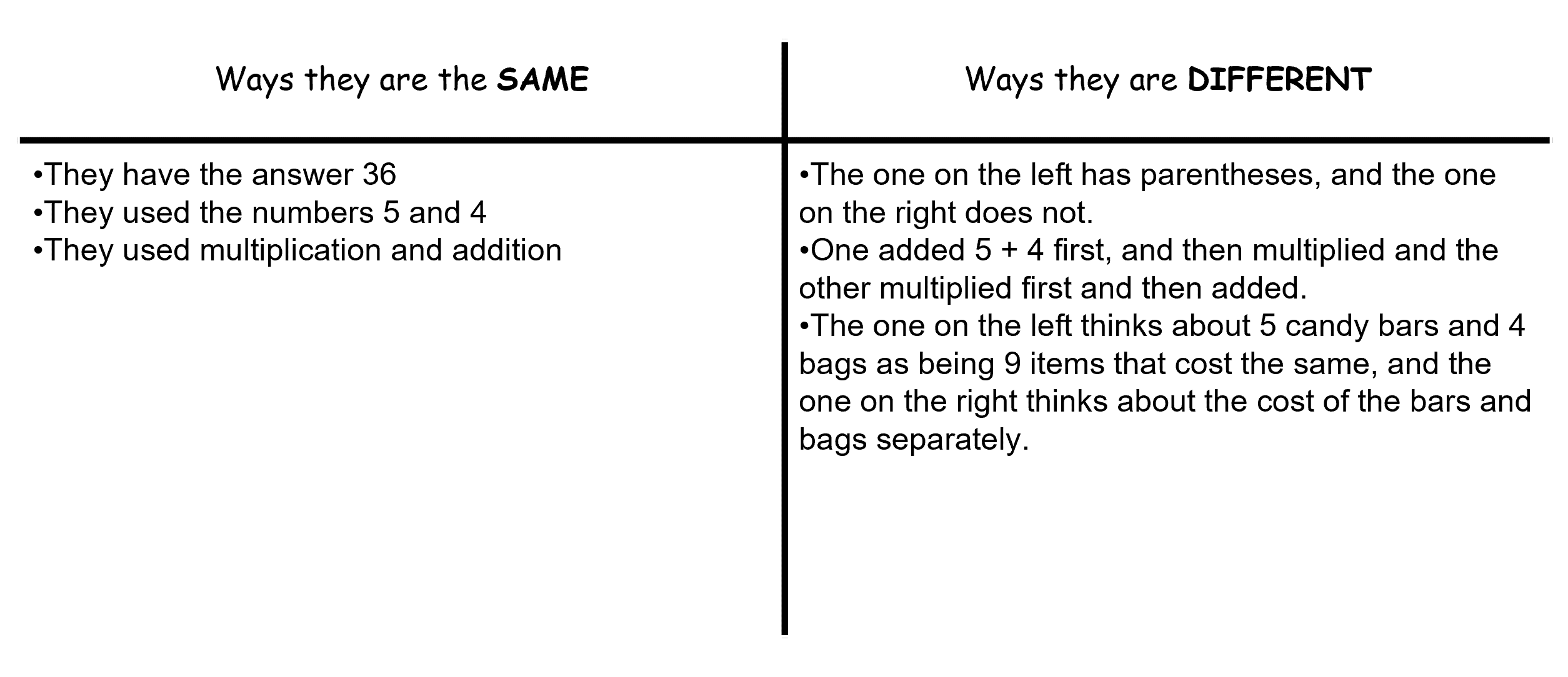
When the idea was shared that the solution strategy on the left could be thought of as grouping items that cost the same thing together, whereas on the right the total for each type of item was calculated separately, there was an “Aha!” moment in the room - a sense of “So that’s why it works that way” surfaced. One teacher even got so excited she came up to the smart board to point out the idea of “items.” Some of us had been using the distributive property, but had not yet had a chance to understand why it works. When we don’t understand the why of a procedure or skill, it is really hard to use that procedure or skill to solve contextual or mathematical problems. Not being able to access the procedure or underlying understanding slows the problem solving process down, can frustrate learners, and make using the procedure in a new context much more difficult.

Once I realized that memorization wasn’t one of my strengths, I learned the strategy of asking why. I learned that once I really understand something, I rarely forget it, and can more easily use and build on it. We need to help our students understand the math they are learning as they develop fluency, and help them connect their developing understanding to their growing fluency.

Best,
Leslie
leslie@magmamath.com