Facilitate meaningful mathematical discourse. Effective teaching of mathematics facilitates discourse among students to build shared understanding of mathematical ideas by analyzing and comparing student approaches and arguments.
-NCTM 2014, p 29
One of the things that immediately stood out to me about Magma Math when I first encountered it was its amazing potential to be a tool for teachers to facilitate meaningful mathematical discourse. Hands down, I’ve never seen anything that could compete! (Teacher Leader, 2023)
The above quote from a teacher leader in a survey echoes my first and ongoing impressions of Magma Math. Magma can be a valuable tool for teachers as they facilitate productive discourse in their mathematics classrooms. In this blog, I’d like to walk through how the 5 Practices framework can be enacted seamlessly using Magma Math to anticipate, monitor, select, sequence, and connect!

The 5 Practices For Orchestrating Productive Mathematical Discourse was initially written by Mary Kay Stein and Margaret Smith in 2011, and it is one of my most used, earmarked, and sticky-noted books! I’ve used it for my own teaching, supporting classroom teachers, teaching Pre-Service Teachers, and as a math leader in my state. When I first encountered Magma Math, I had a similar impression as the teacher leader quoted above, and specifically, I could imagine how Magma would enable teachers to enact the 5 Practices in their classroom. In this Blog, I’d like to walk through how the 5 Practices can be enacted using Magma Math.
First of all, one of the fun features of the 5 Practices is that there are actually 6! Smith and Stein added Practice 0: Planning! So, a complete list of the practices would be:
- Planning: What are my instructional goals?
- Anticipating students’ solutions to a mathematics task
- Monitoring students’ in-class, “real-time” work on the task
- Selecting approaches and students to share them
- Sequencing students’ presentations purposefully
- Connecting students’ approaches and the underlying mathematics
So, let’s walk through the Practices with a Magma lens!
Practice 0: Planning
Not long after the book came out, I was at a conference where I got to hear Peg Smith talk about the 5 Practices. Early in her talk, she shared that they realized almost as soon as the book went to print that there should have been a Practice 0 - Planning!

I am currently working on planning a lesson for a 6th-grade classroom (in a Common Core State) I’m visiting in a few days. The instructional goal of the lesson is for students to be able to reason about and compare unit rates. I went to the Common Core State Standards* via Achieve the Core’s Coherence Map to be sure I know where this is in the standards. I do LOVE the Coherence Map!!! It helps me unpack the standards, know what came before and is coming afterward, and also offers examples of tasks for standards. I think the map is relevant even if you aren’t using the CCSS, as the flow of the math is generally the same, with slight variations here and there. I notice here in the standard that we want students to be able to use tables or equivalent ratios, tape diagrams, double number line diagrams, as well as equations, so when I go to create an assignment in Magma, I know what I’m looking for.
My next step is to build an assignment in Magma. I am going to CCSS Grade 6, the Chapter on 6.RPA.1 and then the sub chapter: Rates and unit rates:
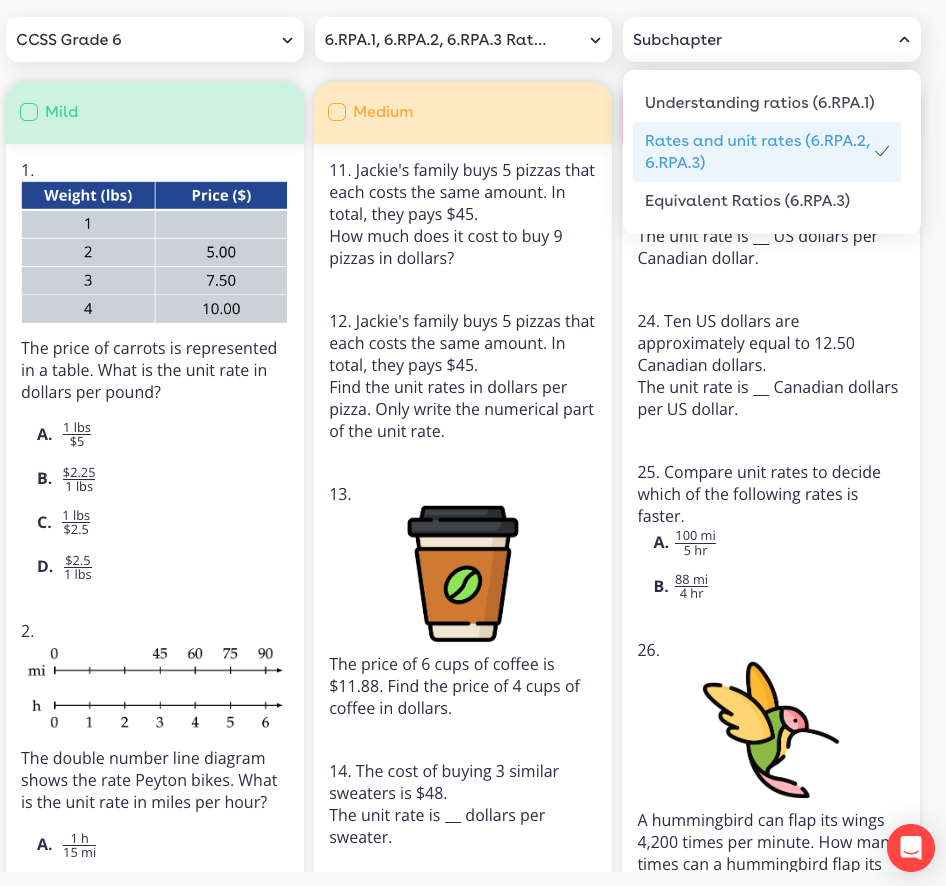
For this assignment, I’m going to intentionally select a few problems in the Mild category, including one with a table, and one with a double number line. I’m going to select one of the medium problems about pizza because it prompts students to find a unit rate, and then the coffee problem because the unit rate is one potential solution path to that. Lastly, I’m going to select one of the dollar conversion problems and the hummingbird problem to provide some higher-level tasks that can be solved in many ways. One of my thoughts is that the two mild problems will serve as an on-ramp for students, that we can engage in a conversation about at least one of the medium problems. The spicy problems leave us room to expand and offer additional challenges.
Practice 1: Anticipate
My next step is to work through the assignment and anticipate how students will solve the problems, especially those that I hope to use as a basis for class discussion. I anticipate that the first two problems are not as meaty for full class discussion - they are there more as an on-ramp for students to be reminded of tables and double-number lines as solution strategies. The pizza, coffee, dollar conversion, and hummingbird problem are more meaningful fodder for conversation. To solve, I click on the three dots on the right-hand side of the assignment and pull down to SOLVE.
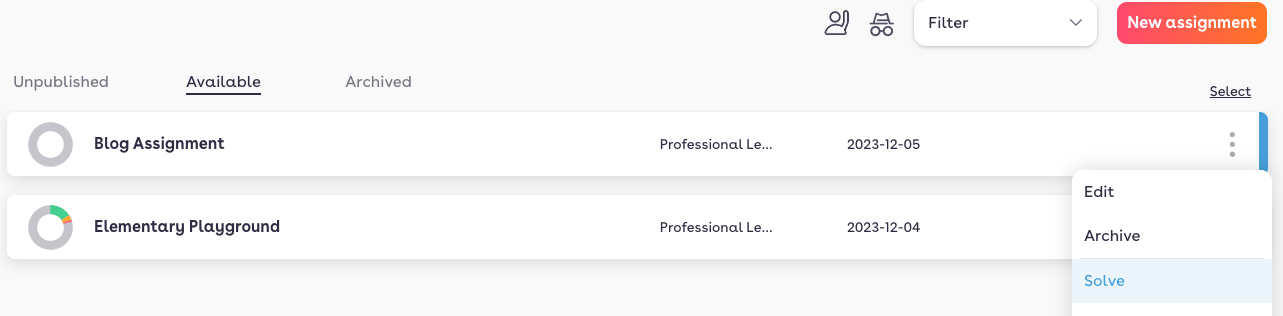
Alternatively, I can open the heat map for the assignment and click on the pen at the top of the column for any of the problems to solve that specific problem.
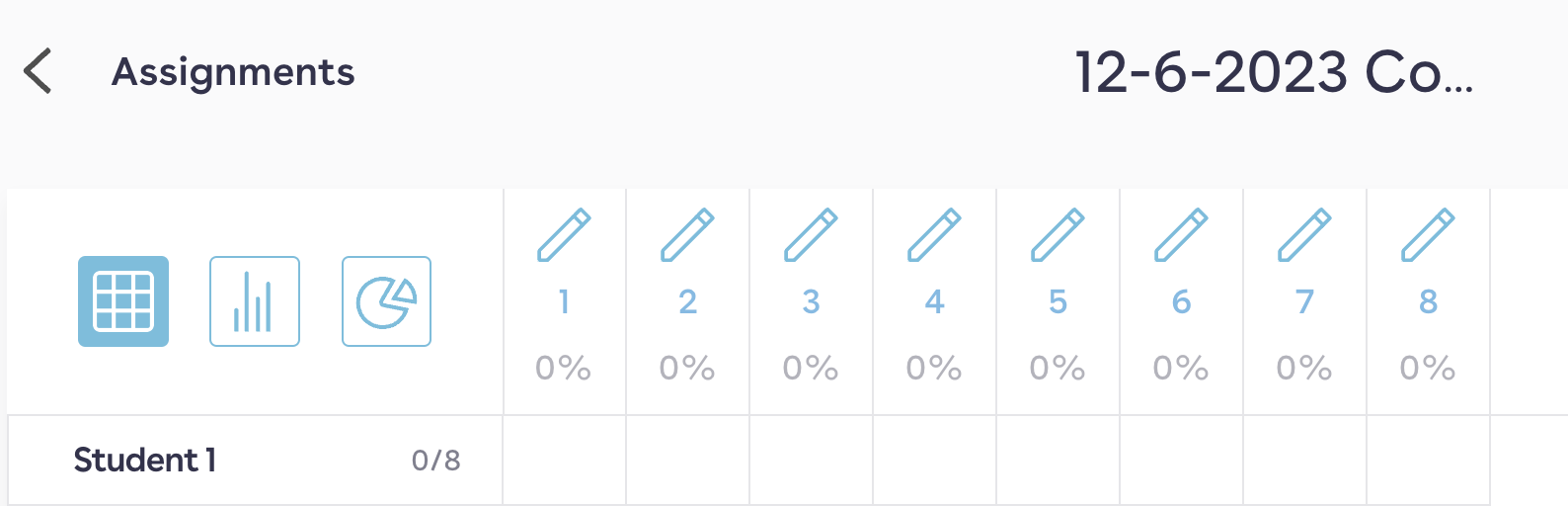
As I solved the problems, I noticed that I have a strong preference for playing with numbers, looking at ratio tables, and not really calling out the unit rate. After working through the problems, I decided to switch one of the problems to one that specifically asks for a unit rate - just to remind students of that strategy.
My planning is getting a bit more specific now. I am planning that the first 2 or 3 problems will serve as “on-ramps” for some students and that we will pause and have a conversation about the Coffee problem, and possibly the Hummingbird problem.
Since I think the coffee problem will be the one that I’m going to focus most of our discussion on, I worked through multiple correct and incorrect ways a student might solve it.
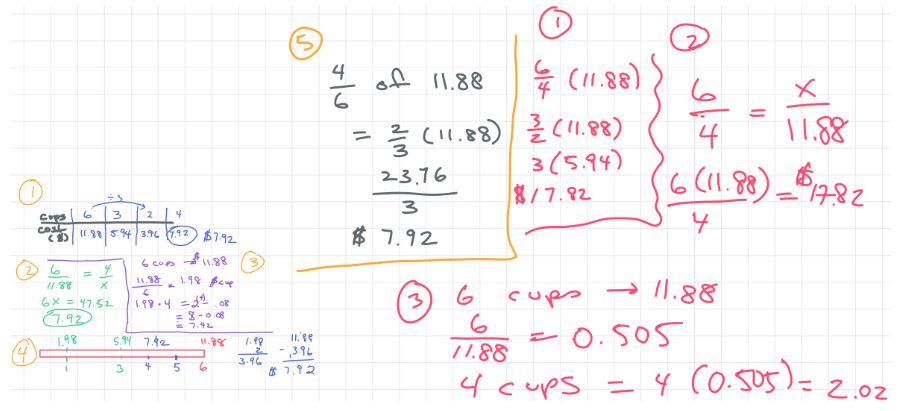
As I think about what I am anticipating, I am hoping that these strategies will surface - and I’m already thinking about how I will sequence the solutions in our discussion.
Practice 2: Monitor
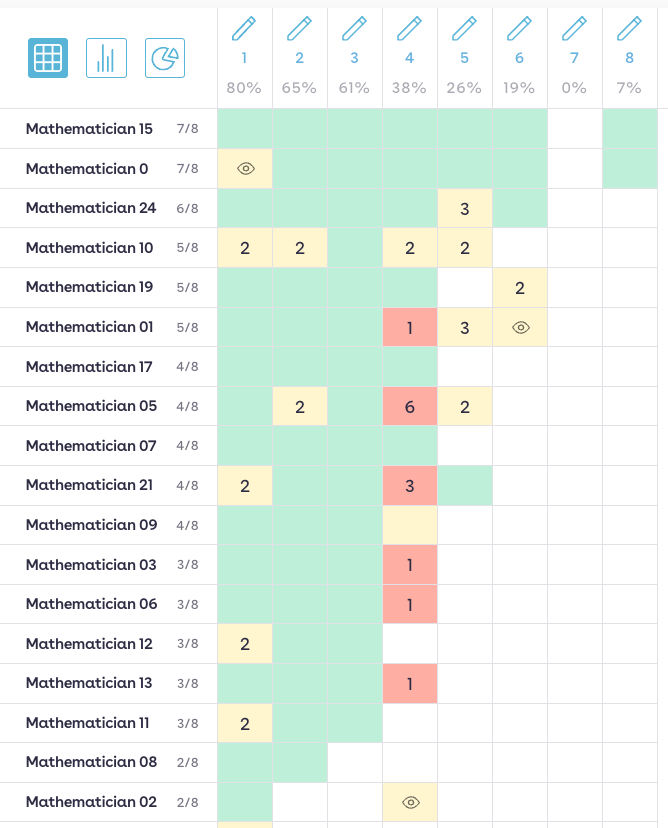
As students work on the assignment, I can monitor in several ways. Of course, wandering around and seeing what individual students are doing in the moment remains an important technique. At the same time, I can monitor the heat map as students submit their solutions.
If a problem seems to be giving students difficulties, I can stop the class and use that problem as a learning opportunity. I am also planning on stopping the class when they get to problem number 4 so we can have a conversation.
My goal is that by having a conversation about the coffee problem, we can make connections between different methods to give students a greater understanding and variety of methods to reason about unit rates.
Practices 3 & 4: Select and Sequence
Selecting is the process of determining which ideas to share and who to have share them (i.e. whose work to highlight.) Often, when I’ve led a conversation of strategies in the past, it has turned into a mathematical “show and tell.” I’ll ask the class, “How did you solve it?” and/or “Did anyone solve it in a different way?” … and then someone’s hand will go up, and they share their solution. The problem with that way of facilitating the discussion is that I don’t know if the method the student will share will move the thinking of the class forward. I’ve had students share the same method that we just discussed, jump in and share a very abstract method at the beginning of our discussion, or go down a rabbit hole that is quite hard to follow. When a more abstract method is shared first, some students won’t be able to understand it without a more concrete approach as an on-ramp.

Another thing I want to consider is students’ mathematical status. As I select student solutions to discuss, I strive to give each student opportunities to have their work centered, rather than rely on the students who are fastest and most eager to raise their hands.
While students are still working, I can look at the student solution view and select 4 student solutions for the students to consider for conversation.
For this discussion, I want to build from most concrete to most abstract, and I would like my students to consider the solution Student 4 used as an example of proportional reasoning. I think in this case, I would start with Student #5, then #3, and then #2 as they build the same strategy with increasing abstractness. Then I would project student #3 and student #4 and ask students to consider what is the same and what is different.

Practice 5: Connecting
Smith and Stein write that Connecting may be the most challenging of the 5 practices because it calls on us to craft questions that make the mathematics visible and understandable. Questions we ask our students have to go beyond clarifying and probing and instead focus on mathematical meaning and relationships.
As I am thinking about connecting student solutions to each other and also to the underlying mathematics here, I want all of my students to understand the idea of the unit rate. I also want them to understand how proportional relationships work.

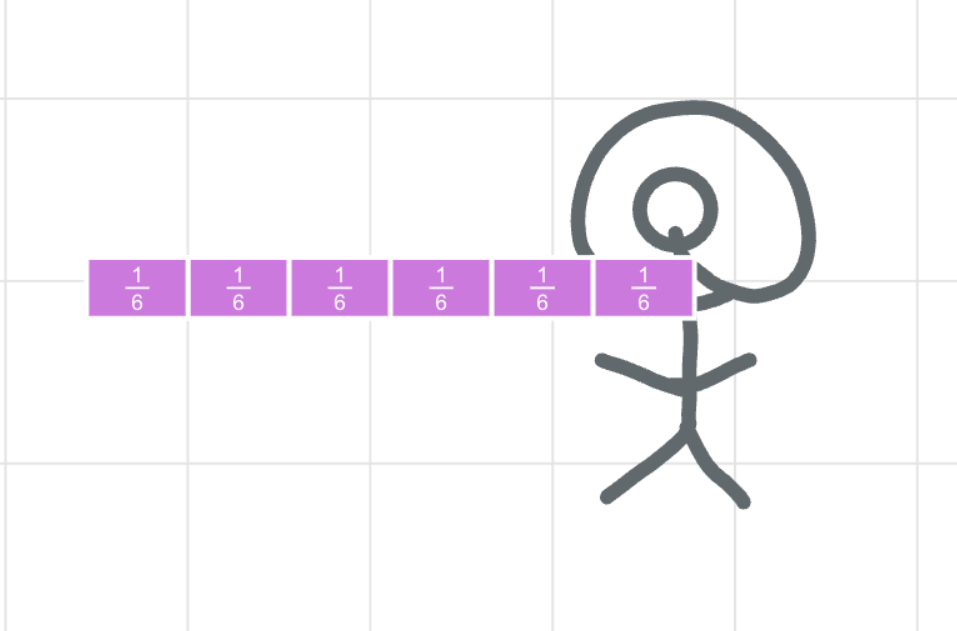
Student #5’s solution may help students understand how we get the unit rate. I would play that solution back, stop when the fraction bar is constructed, and ask students why Student #5 might have done this before playing the rest of the solution.
Then, we could connect this solution directly to Student #3’s solution. Why did we divide by 6 and then multiply by 4?
Student #2’s solution has several ideas I want to connect. How is it the same and different as Student #3’s solution? In #2’s solution, I see both a proportion that we should unpack, and also the statement x = 46(11.88). I would like students to make sense of the fraction 46 in this context.
Lastly, I would show them Student #4’s solution and ask them to think about how it relates to the other methods. Where do they see the 46? Where is the unit rate? How are these methods the same and different? When might you prefer to use one instead of the other?

Closing thoughts
I have been aspiring to incorporate the 5 Practices into my teaching since I first encountered them. Colleagues and I have collaborated on how to infuse them into professional development we facilitate - both as we are teaching math content to teachers and as a pedagogical practice that we have helped teachers learn to enact.
When I first encountered Magma Math, I had the sense that it could have been developed with the 5 Practices in mind. Magma supports us all along the way - from planning & anticipating, through monitoring, selecting & sequencing, all the way to connecting as we facilitate meaningful mathematical discourse with students.
Best,
Leslie
leslie@magmamath.com



.jpg)

%20(1).png)



