Just before summer break I had the wonderful opportunity to be in Sweden and talk with colleagues at Magma Math about how we learn and teach math. One morning, I got to visit a grade 2 class with colleagues from Magma. In our visit, we were reminded of the importance of the progression of concrete to pictorial to abstract in learning. Students need multiple opportunities to use physical objects as they learn before they progress on to using drawings and pictures such as virtual manipulatives. Only then are they ready to work with math symbolically.
Specifically, we were reminded of how powerful it is to incorporate physical manipulatives into math learning and teaching. The students were working an assignment that included adding and subtracting within 100. Some of the problems did not involve regrouping, but a few required that students “carry” or “borrow.” Here are two of the problems that we were working on.

As the students were working I realized that some of them were unclear about what exactly is happening with regrouping. In particular in the problem 342 - 305 was generating some interesting solutions. Here are three that had me wondering.

I walked around the room and asked some students how they were thinking about these problems and decided that it would be interesting to have a whole class conversation about 342 - 305. I also noticed that there were base 10 blocks on a shelf! So, I passed the blocks out to the groups - a handful of ones, tens and hundreds, and as usually happens in a classroom, the students started playing and building with them! Towers and houses were built, and one student created a butterfly.
After a little while, we got the whole class's attention, and I asked the groups to use the blocks to show me how they would do 342 - 305.
Most groups built 342 with 3 hundreds blocks, four tens and two ones, and then thought about how to “take away” 305. Other groups built 342 with the blocks and built 305 with the blocks and then worked to figure out how much bigger 342 was than 305, finding the difference.
After groups had talked for a while, we had a whole class conversation, linking the models with blocks to the work the students had shown in Magma. We discussed that one way to think about this problem was to take the 3 hundreds away first, which left us with the problem 42 - 5. (It would have been interesting to discuss whether this strategy would always work.) I asked students to talk with a partner about how they would show 42 - 5 with blocks, and after a few minutes of turning and talking, one student, Milas, came up and shared how he and his partner did it using magnetic base 10 blocks that stick on the white board.
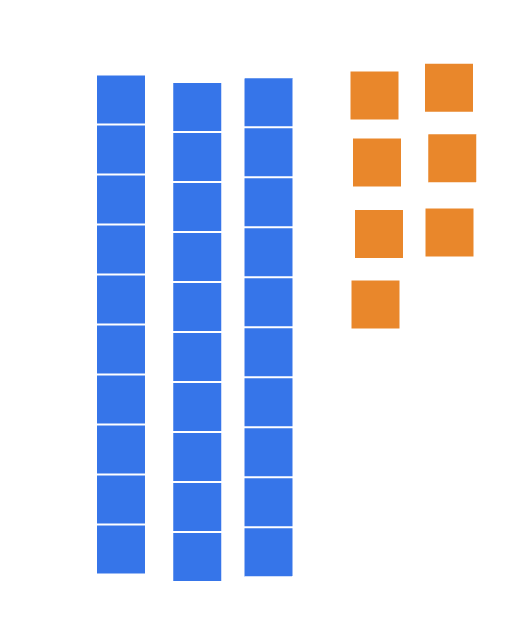
The model:
We started with 4 ten blocks and 2 ones.

First, Milas took 2 away from the 42, leaving him with 40 tens.

Then there was a moment of thinking as he had to remember what more he needed to take away before he changed one of the tens into 10 ones…

...and then took away 3 more ones, leaving him with 37.
As I write this, in reflection, I realize that it is very natural to take away what you “can” first before the stage of “making change” and breaking a ten into ones. AND this requires using short term memory to remember what more you have to “take away.” This feels like something to explore with students and unpack as we support them in developing their understanding of regrouping.
After working with the physical blocks, we showed the students how to use the virtual base 10 blocks in Magma Math. It was pretty exciting for the students, and for the Magma team because we had several of the developers in the room on the visit. It was helpful and inspiring for them to see how students use base 10 blocks.
We wound up not having time in the class to explore the strategy of comparing the two numbers, but I’ve been playing in Magma to see what it might look like. Here are the numbers 342 and 305 in Magma Base 10 tiles.
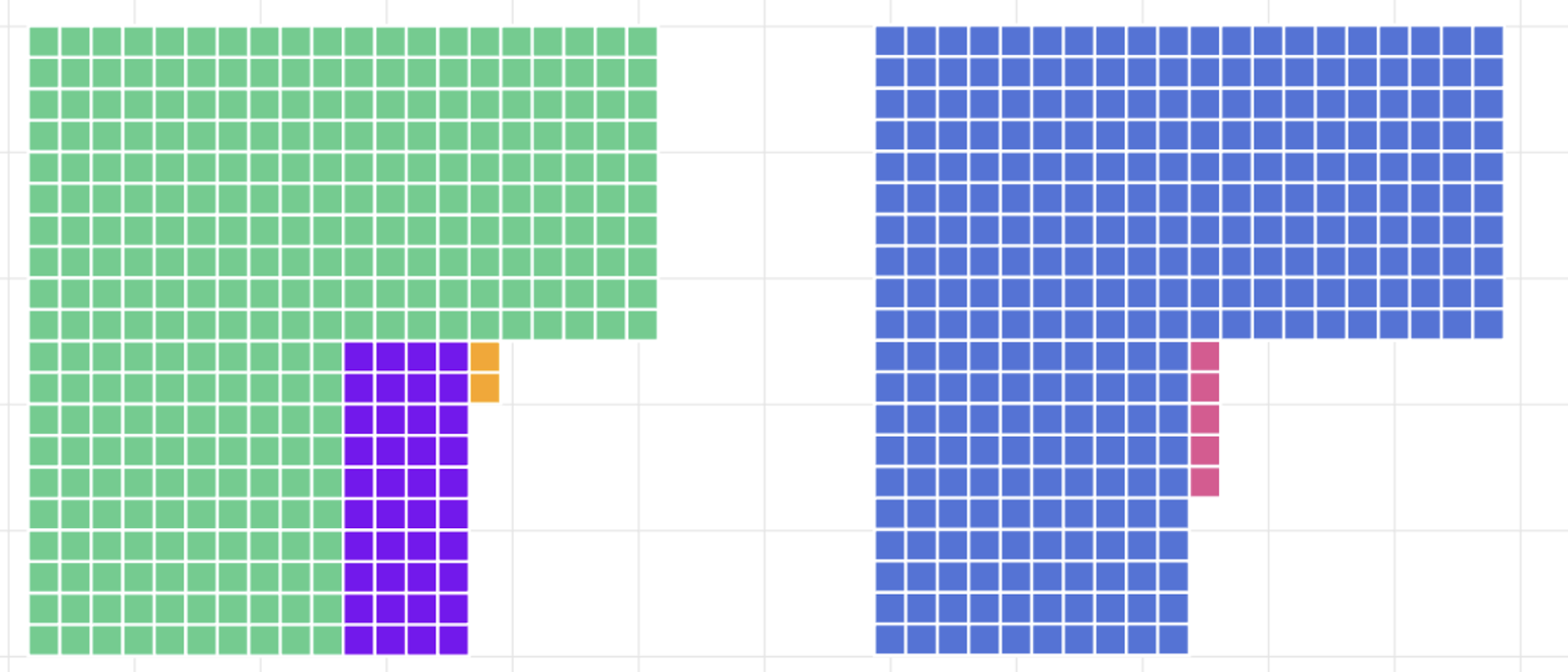
And here, I have dragged the 305 tiles on the right onto the 342 tiles on the left. The remaining purple and orange tiles are the difference in size.
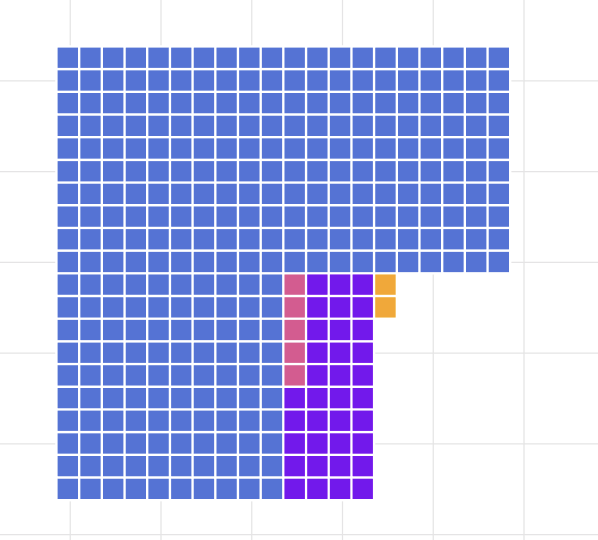
In the visit, we were all reminded of the importance of starting with concrete, physical manipulatives before moving to symbolic and then abstract. On the subway on the way back to the Magma office, my colleague, Mattias suggested the title of this blog, Get Physical First!



.png)
.png)




