The second Effective Mathematics Teaching Practice is Implement Tasks that Promote Reasoning and Problem Solving. When I observe a classroom with this practice in mind, I am often struck by the art of teaching. The teacher seems to move gracefully, making decisions and responding, the students are highly engaged, leaning in and discussing, perhaps even arguing about the mathematics. It might almost look like the teacher’s job is easy, but the reality is that there is a great deal of planning and decision-making that happens before a lesson starts that exemplifies this practice. The teacher must choose a task with care, and plan how they will set the task up and keep it on track during the lesson.
‍

Choosing a task for students that will further the goals I have for the lesson is an important first step. In Magma Math, I might navigate to the standard(s) that I’m working towards and select a problem in the spicey column. If I want my students to work effectively in small groups, I want to select a problem that is challenging enough that they need collaborators to help them solve it. I want to aim for a problem or small set of problems that are at least DOK 3, which also have multiple entry points and solution methods. I might even choose a task that doesn’t have “one right answer!”

‍
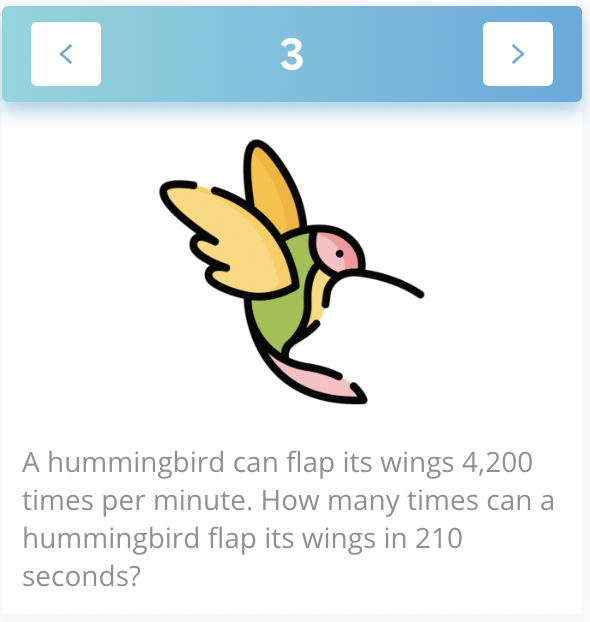
A favorite problem of mine in Magma Math is the hummingbird problem because there are so many ways for students to access and solve it.
‍

In their 1998 book, Margaret Smith and Mary Kay Stein wrote:

"Tasks that ask students to perform a memorized procedure in a routine manner lead to one type of opportunity for student thinking; tasks that require students to think conceptually and that stimulate students to make connections lead to a different set of opportunities for student thinking."  (Stein & Smith, 1998, p.269)
‍

Smith and Stein went on to classify tasks into four levels of demand:

• Low level - (memorization)
• Lower level - (procedures without connection)
• Higher level demands (procedures with connection)
• Higher level demands (doing mathematics)

‍
To implement tasks that promote reasoning and problem solving we want to spend significant time focusing on higher level tasks. The hummingbird problem can be an example of a higher level demand task, ie. procedures with connection - or even a higher level demand (doing mathematics) depending on the instructional goals, the math my students already know, and most importantly, how I facilitate the task. 

Choosing the task is just the beginning. How do we facilitate the task so that it continues to be a highly-cognitive demanding task throughout the class session?

A few years ago, Peg Smith and Mary Kay Stein published the Math Task Framework in which they wrote that the tasks in the curriculum and the tasks as set up by teachers might both be very high quality and well planned, but when implemented by students and teachers, the cognitive demand of the task was often reduced - either by the students trying to get help rather than persevere, or by the teacher over-scaffolding or answering questions the students might be able to answer themselves. 

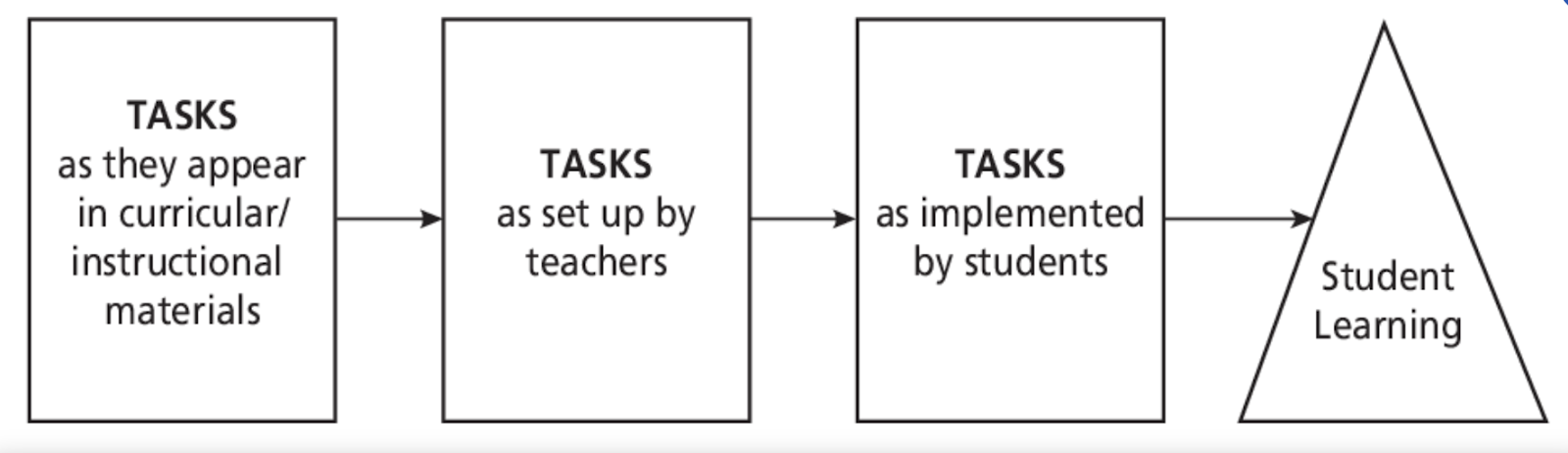
This information means that we need to plan before we implement the task. How will we offer just the right amount of scaffolding so students all have access and feel safe taking the risk to share their mathematical thinking while also not doing the work for them?

Best,
Leslie
leslie@magmamath.com