There’s strength in students showing their work, for them and for you. From their end, their solutions act as arguments that justify their final answers. Even if their final answers are wrong, it gives them the opportunity to be heard and understood. For you, as a teacher, solutions can give you more familiarity with your students, their knowledge, and their mistakes.
Errors in subtraction are found to be the most common within the four operations. Since we have gathered a lot of handwritten solutions on Magma Math, we chose to analyze the solutions to a specific subtraction problem: 431−163. This problem involves subtracting two 3-digit numbers and requires ungrouping when solved using the standard algorithm. In this problem, ungrouping is necessary when subtracting both the ones and tens digits. We have intentionally chosen this problem due to its complexity and potential for more variations of errors. This problem had 2,457 solutions and 939 wrong answers. We have looked closely at those wrong answers and analyzed the most common mistakes.

Inversion errors
By combining the results of 60 years of research on common errors, Coleen Blankenship found that the most common and persistent type of subtraction error is inversion errors. This occurs when students confuse which digit should be subtracted from which. Our data support this observation. The most common error to our subtraction problem is one type of inversion error.
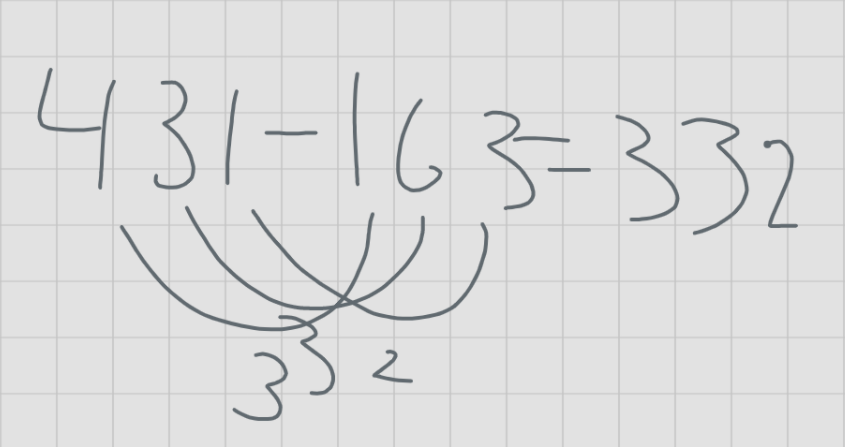
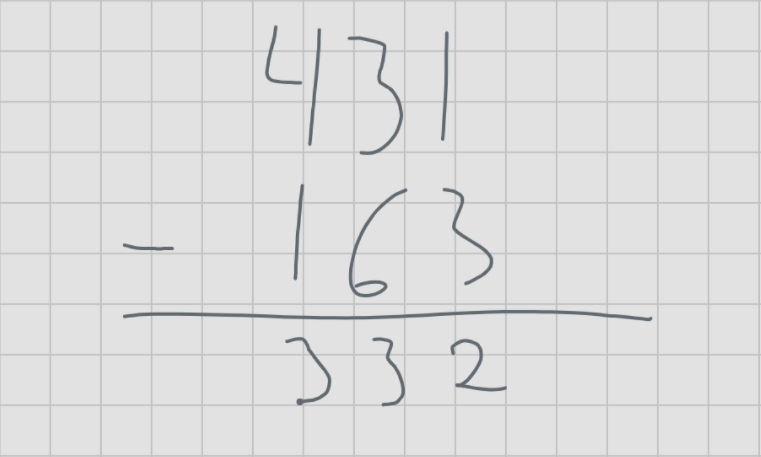
In these two examples of student solutions, students subtract the smaller digit from the larger digit, regardless of which number is the minuend and which one is the subtrahend. This was the most common error we found in our data, with about 22% of wrong answers being this inversion error.
Ungrouping, then forgetting
The second and fourth most common errors are found to be quite similar. In these solutions, students carried out the ungrouping step but forgot about it when they moved on to the next digit.
The second most common solution we found to our subtraction problem is 278. In these solutions, students succeeded in ungrouping the tens place to subtract the ones digits, but did not take in account ungrouping when they subtracted the hundreds digits.
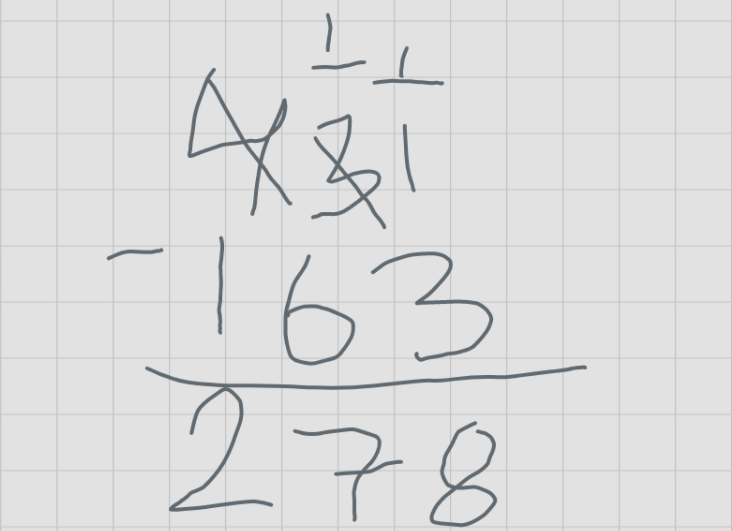
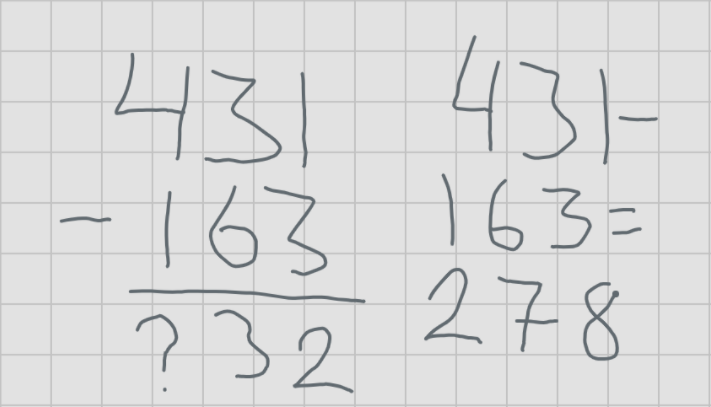
The fourth common error is 269. Here, students succeeded at ungrouping for the ones subtraction, recalled the ungrouping when subtracting the hundreds digits, performed the ungrouping for subtracting the hundreds digits, but failed to recall the ungrouping when subtracting the hundreds digits.
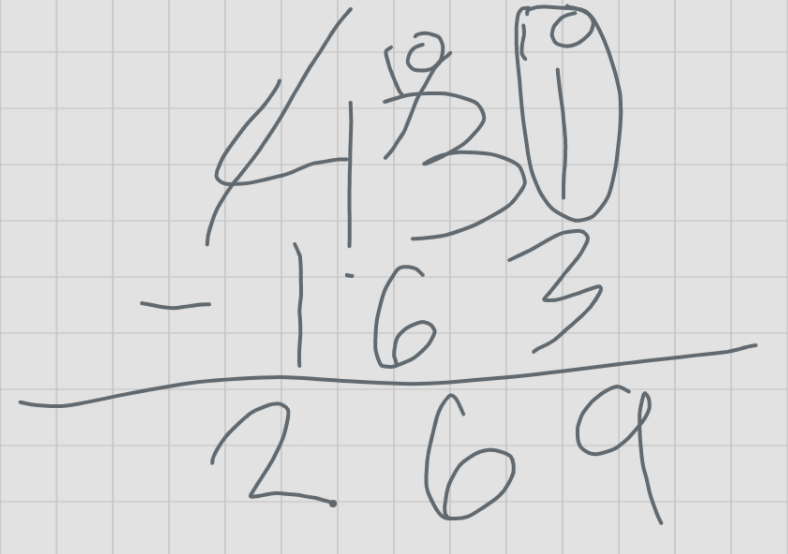

Adding instead of subtracting
The third most common mistake students made was to perform an addition instead of a subtraction.


Is this mistake because of a conceptual misunderstanding, or have the students just overlooked the subtraction sign? To answer this question, it is important to look at the context. Was this problem placed in an exercise that includes both addition and subtraction problems? Have the students who answered this problem this way also answered other subtraction problems the same way? If you find your students making this mistake, you will be able to figure out the reason based on the context of encountering the problem and how often the error is repeated.
The frequency of a student repeating specific errors can tell us a lot about the reasons why they are making it and what to do about it. If one of your students makes a random error by the end of every exercise, and another student makes an inversion error in almost every subtraction problem, you can decide to intervene in different ways. Therefore, understanding exactly how your students are performing is necessary to help them reach their potential. We have seen how looking at students’ work can provide insights into their misconceptions, and you can do the same with your own students. Even though you may not be in the same room as they are, looking at their handwritten solutions is a great way to connect with them, understand them, and help them.





%20(1).png)


