In today's evolving educational landscape, the responsibilities of fostering a dynamic and interactive learning environment are more critical than ever. Educators are tasked with developing curriculum strategies, implementing effective teaching practices, and ensuring that students are not just passive recipients of knowledge but active participants in their learning journey. At Magma Math, we understand these challenges and are dedicated to providing innovative solutions that enhance student engagement and deepen understanding.

A key principle of effective math instruction is centering student thinking. This approach empowers students and allows teachers to leverage student insights to drive learning. By selecting and sharing student work for classroom discussions in the platform, teachers can spotlight student thinking, fostering a collaborative and reflective classroom environment.

Inspired by Dr. Peter Liljedahl’s concept of Building Thinking Classrooms, Magma Math takes this idea further. We help teachers defront the classroom, shifting the focus from teacher-led instruction to student-centered learning. This shift mobilizes student knowledge and supports the consolidation of understanding from the bottom up, creating a more inclusive and engaging learning experience.

But what does this look like in practice? How does centering student thinking with Magma Math translate into real-world classroom benefits? Let’s explore how our platform supports this transformative approach and the tangible impact it can have on your students.

Defronting the classroom‍

Dr. Peter recommends defronting the classroom as a step that has an immediate effect on both students and teachers. When desks are “defronted,” placed in groups of three facing a different compass direction, students have room to walk and work around the perimeter of the room, change happens. Students think more, collaborate more, and learn more while teachers talk less. In the adoption of defronting within classrooms, Dr. Peter and his team saw a decrease in how much teachers demonstrated things on the board at the front of the room, and instead circulated more throughout the room, facilitating conversations among students. 

There are times when we want our students to consider one or more student solutions via Magma, and I have become fond of saying that when we display student work via Magma, we are “helping teachers center the room with student thinking.” The teacher may not be anywhere near the board where the math is being projected, and students are noticing, wondering and discussing what they see in their classmates' solutions. 

‍

Mobilizing student knowledge‍

In a Thinking classroom, Dr. Peter writes that knowledge is mobilized in one of three ways:

1. Members of a group going to other groups to borrow an idea to bring back to their group
2. Members of a group going out to compare their answer to other answers, or
3. Two (or more) groups coming together to debate different solutions

Knowledge is also mobilized through frequently changing random groups as students share their knowledge and problem solving ideas from members of a previous group with a new group. Additionally, knowledge can be mobilized when students notice what their classmates have written on their surface and then incorporate that information into their own thinking and work.

We can further use Magma to mobilize student knowledge when students are working Check Your Understanding (CYU) or other assignments in Magma. 

If my students were getting stuck on a problem, one strategy might be to display student work from a previous problem that can act as a scaffold to the next problem. In this case, say that some students were stuck on this area problem.

‍

‍

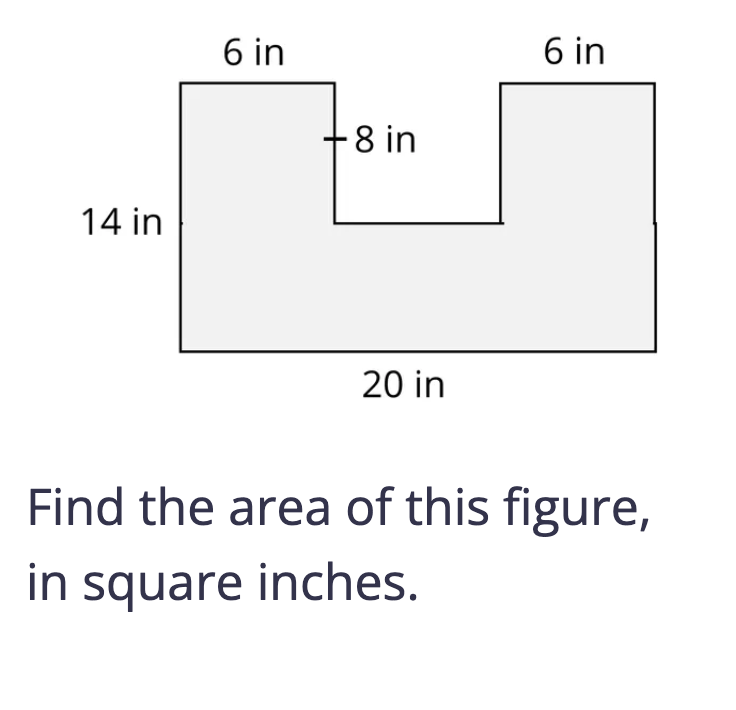
One teacher move I might make is to have a class conversation using the Same But Different routine with these two student solutions to a previous problem as a way to provide some scaffolding based on student thinking from my classroom. 

‍

‍

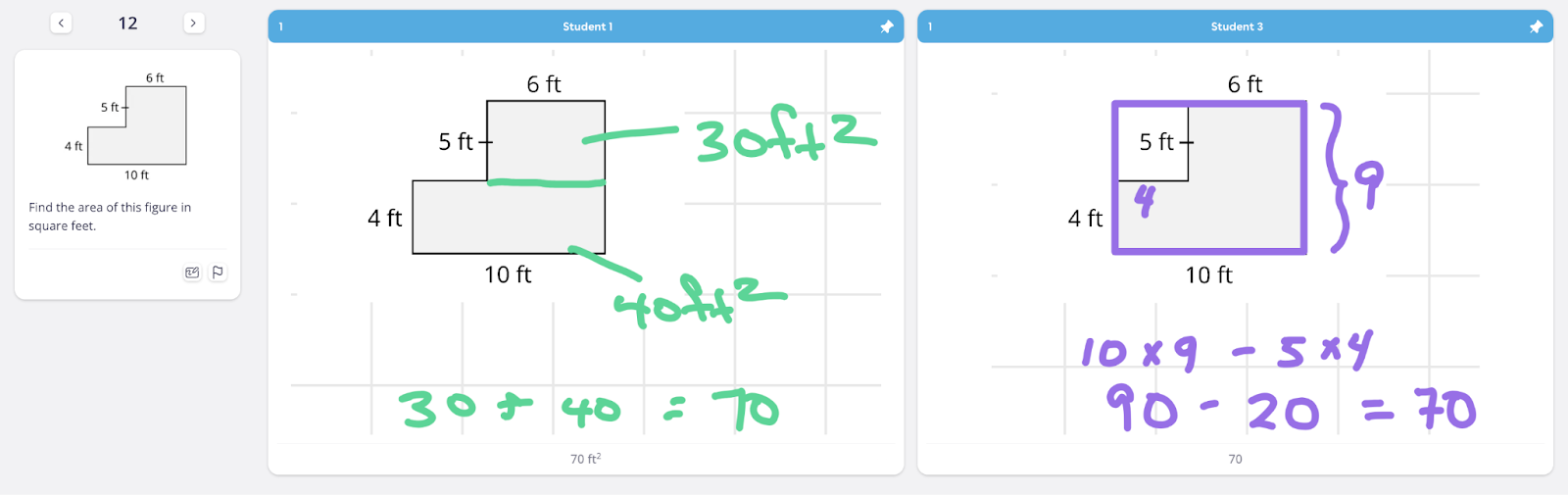
These two student solutions to the area problem could be used in a Same But Different routine to help students develop flexible strategies for finding the area of composite figures, including dividing the figure into smaller components and finding the area of a larger shape and subtracting the empty space. By exploring their classmates' solutions to a different problem, knowledge within the classroom is mobilized. Students can then experiment with and try out different strategies on new problems.

Consolidating understanding from the bottom up

The third way that centering student thinking can play a role in a Thinking Classroom is by using student solutions as the focus of discussion of a problem while being intentional about the order in which student solutions are sequenced. This strategy is tied closely to the 5 Practices for Facilitating Productive Mathematical Discourse from Smith and Stein in which teachers anticipate what students will do with a math problem, monitor their students’ work, select which problems to discuss, determine the ideal sequence in which to discuss student solutions, and make connections between the solutions and to the underlying mathematics. 

Dr. Peter advocates consolidating from the bottom, starting with presenting solutions that all students go to, rather than starting off by showing the solution(s) that only a few students generated, or perhaps even the solution the teacher did, in hopes that students will learn to do math by seeing the most sophisticated or elegant solution. His research demonstrated that the most effective method for maintaining student engagement while consolidating from the bottom is to use student work to lead a detailed discussion of the task(s) and solution(s), to work through the different layers of the solution. 

Dr. Peter’s research focused on work students have done in groups on vertical surfaces. At Magma we believe that this can also be an effective way to consolidate when teachers want to focus on work students have done in Magma. Teachers can consolidate understanding from a specific problem in Magma, by pinning the solutions they want their students to consider. Teachers can do this in the moment, but also during planning time or even perhaps during a Professional Learning Community meeting. If I want the solutions considered in a specific order, I can pin them in that order.

The power of these three teaching strategies is that they center student thinking. When students see their own and their classmates' solutions shared and discussed, they realize that their solutions and thinking matter. It is inspiring to students to have their work shared with the class, even anonymously, promoting positive mathematics identity and agency!