Effective teaching of mathematics engages students in making connections among mathematical representations to deepen understanding of mathematics concepts and procedures and as tools for problem solving.
- NCTM 2014, p.24.

Have you ever considered how you understand a mathematical idea? Consider these situations:
‍

• I have 7 cookies to share fairly among 4 children.
• My dog requires ¾ of a pill twice a day and I’m taking her on a 212  week trip.
• I’m making a quilted pillow with a pattern. The center of the pattern is a square that is 6 inches on each side that will be surrounded by right isosceles triangles. The hypotenuses of the triangles line up exactly with the sides of the squares.
  ‍

For each of these, what did you imagine as you considered the situation? How did you represent the situation in your mind’s eye (or on paper)? Did you sketch a picture? Grab some manipulatives (or a piece of paper) to recreate the situation? Write an expression or equation?

In Adding it Up, the National Research Council wrote “Because of the abstract nature of mathematics, people have access to mathematical ideas ONLY through the representations of those ideas” (NRC 2001). Even the sentences I used to describe the situations above are representations! How we support math learners through the use of representations, by connecting representations, and then supporting them in selecting, using, and moving fluidly between representations is of vital importance. Ultimately, our goal is that students will view representations as tools that they can use to help them solve problems, rather than as an end in themselves.

There are five types of representations that we typically think about in math teaching; visual, symbolic, verbal, contextual, and physical. These are often shown connected in a diagram like this.

‍
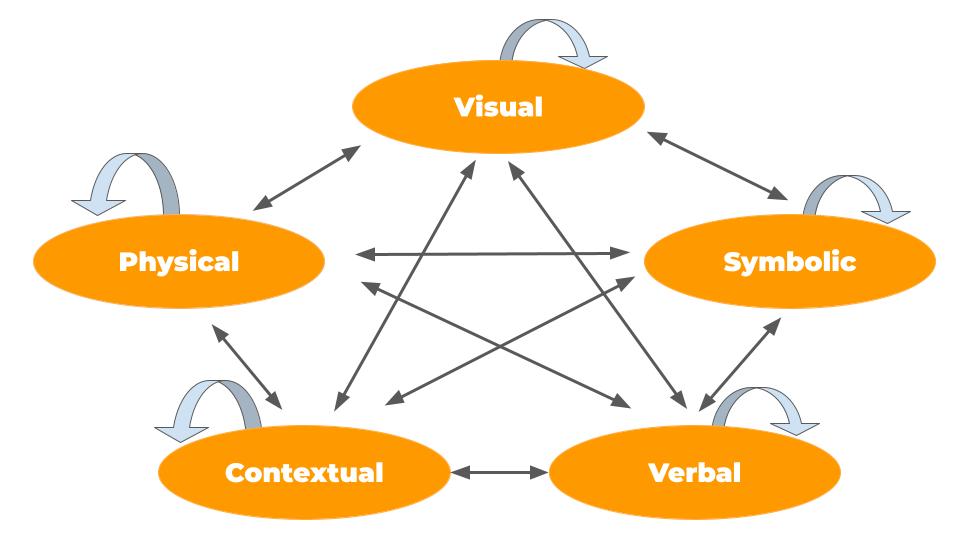
The key is how we help students make connections - both between different types as well as within a type of
representation. Principles to Action (NCTM, 2014) lists three specific strategies to help students develop representational competence:
‍

1. Encourage purposeful selection of representations.
2. Engage in dialogue about explicit connections among representations.
3. Alternate the direction of the connections made among representations. 

Magma Math can support us as we make connections with students between and within representations. Consider this fun problem:

At a first aid training, there were 24 teachers, 16 flight attendants, and 36 lifeguards. Participants were divided into groups. All groups should include equal number of teachers, equal number of flight attendants, and equal number of lifeguards. In addition to this, each group must have less than 20 participants. What is the number of groups that the participants can be divided into?

‍
And this sample of student solutions.

It is worth noting that many of the other Math Teaching Practices come into play here such as decisions about how I will select and sequence student work in the discussion, as well as thinking about how we will connect representations.  I notice that Students 6, 4, and 12 have more concrete representations, and I might want to start the conversation looking at how those specific representations are related in order to provide more access for more of my students. 

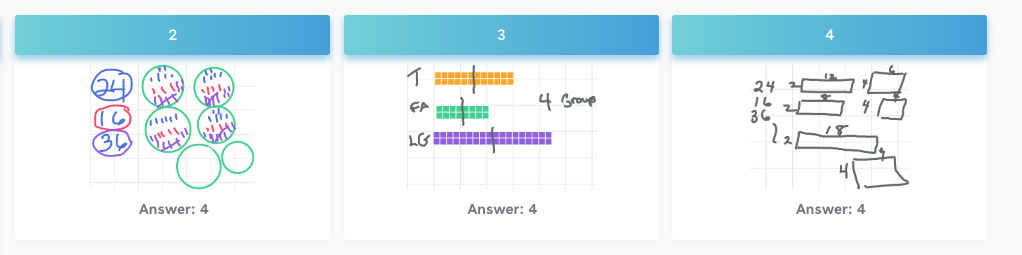
What purposeful questions might we pose as we help students make sense of these solutions and how they are related? I am curious about how Student 2 decided to draw 6 circles but only seems to use 4 of them. And how did Student 3 put their solution together? I would replay Student 3’s solution for the class, pausing to discuss the decisions they made.

I would also make connections between Student 3’s and Student 4’s solutions. How are they the same and how are they different? If Student 3 had rearranged the tiles instead of dividing them in half with a line, would their solution be more similar to Student 4’s solution?

Next I might pivot to the representations that are purely numerical (symbolic) and ask students to make connections between the various methods. Where does the 4 come from in each solution? Why is that the LCM (is it?)? (and what is an LCM, and what is a GCF? And how do we keep those two straight? What do they look like visually?

Lastly, I would ask students to make connections between the types of representations. 

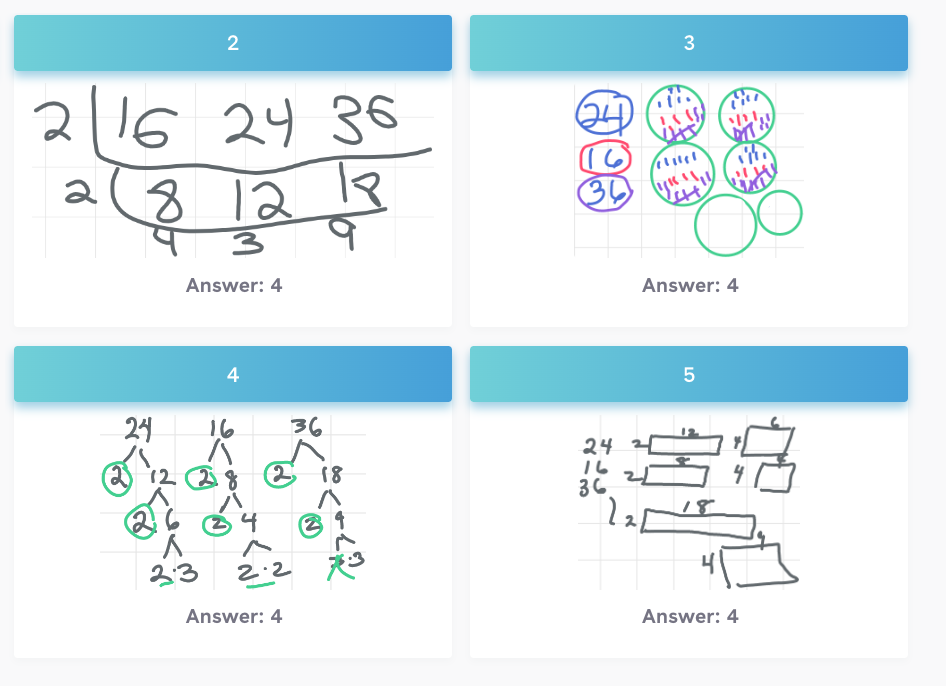
How do the two 2’s that show up in Student 2’s and 4’s solutions show up in Student 3 and 4’s solutions? Why start with 2? Does this always work?

Next steps involve encouraging students to use multiple forms of representations to help them make sense of the mathematics. I love to ask students to try the next problem using someone else’s representation style just to “try it on.” 

I think choosing representations and playing around with them is one of the fun, more playful aspects of mathematics. It is a chance for students (and us) to get creative! And sometimes, even when we know the answer, playing around with a new representation or two might give us insights into new ideas and create even more interesting mathematical moments!