Tell me a little bit about your journey into teaching.
I always wanted to be a teacher and growing up, I liked learning about math. I decided to continue my learning in college and I got my BS in Math from UC Santa Barbara. I came from Mexico to the US in the 4th grade and I didn’t know any English. The only thing that made sense in school was math and this allowed me to connect to my classmates, I could point at diagrams and numbers and we understood each other! During college I worked for a program where I was placed in classrooms to support ESL students in their math classes. That’s where I realized that teaching was my career path. After a year off from college I went back and got my teaching credential along with my Master’s in Education and took a job teaching in South Los Angeles.
I worked at a school in Huntington Park where I grew up. I wanted to give back to my neighborhood, as I felt there was a disconnect between what students need and the support they receive from schools. My goal has always been to teach math and advocate for students' needs. In my community there are lots of first generation, undocumented, and EL students. Many of them are gifted and talented and they get overlooked as mathematicians because schools often place all their emphasis on addressing the needs of poverty and English comprehension.

I know this from firsthand experience. In school I got English support, but I did very well in my math classes. I got to skip grade levels in math even though I was behind in English. I do believe that language has a big role in how students learn math, but if you can give language support to students as well as chunking, scaffolding, and translations, they can access the math. I’m always looking for ways to help my students achieve in math regardless of what other needs they have.
Tell me about something you do with students to be creative and work on their problems solving skills.
I have been assigning Problems of the Week (POWs) since I started teaching. These problems are exploratory, open-ended problems that students get a week to work on. The point isn’t to find a final solution, but to work out as much of the problem as possible. I have used POWs in high schools but more recently I started working with elementary and middle school students to complete POWs. This summer I’m working with 4th graders and doing POWs online and it’s been great! POWs are really flexible like that! You might build in more student support depending on the grade level you teach, but students will take a POW and really run with it, especially when they’ve been implemented into your classroom routine.
Do you use POWs to introduce new content?
Some of my POWs are essential assignments in our thematic units. Other times, if students are learning a really dense math topic, the POW serves as a break from the content and allows students to process the math they’ve been learning. They can also apply their skills to a different problem. I would say that you can use a POW to target a specific skill. POWs are based on finding patterns, playing mathematical games, or are theory-based. Last year my students spent a week playing and revisiting Linear NIM because we needed a break from new content.

I think POWs are a great way to address the 8 Mathematical Practices- students work on recognizing patterns, using mathematical models, and math writing. The POW culminates with a write up, where students explain their process and any tools they used such as graphs, diagrams, and tables. The whole POW process involves multiple representations- can students represent the problem situationally, graphically, numerically, and algebraically? POWs build up all of these math skills without the students even knowing!
You mentioned a write-up, what does that look like?
The POW write-up has five components: problem statement, process, conclusion, extension, and self reflection. The write up is a way for a student to show off their process in a way that makes most sense to them. I usually make the Problem Statement the first checkpoint in the POW, which is a summary of the problem. This forces students to read and makes sense of the problem before getting started. I know when a student’s Problem Statement doesn’t make sense, that student won’t understand how to get started. Oftentimes it is a language barrier or some other block that is preventing the student from understanding, and I can use their problem statement as a way to figure out how to support each individual student.
How do students write about their process?

The process can look different for every kid. Students who like to write a lot will write pages and pages on what they tried, kids who are visual will create organized diagrams. Some students like to make posters or slides to show their work. I like for students to communicate in the way they feel most confident. The goal of the process is for students to write everything they tried, including the parts that didn't work. Writing conjectures and why something doesn't work is what math is to me.
Is it hard to get students to write about their ‘mistakes’?
It varies greatly on the mindset a student has in math class. In the beginning, students who are working on their growth mindset might be hesitant to write about what does not work. From my experience, I’ve noticed that students are trained to not submit mistakes on final assignments, so they are hesitant that submitting their ideas that turned out to be wrong will somehow negatively affect their grade or their status in the class. Sometimes I give students a table to record their attempts to ensure their process includes multiple attempts. Other students may have the mindset that all evidence is good evidence, and are more willing to share what I call “boo boos” in their work. It's a process getting students to that point.

I think it is important to model mistakes yourself- I will model POWS to students and share what I've tried and what didn't work for me. I’ve even done POWS where I haven't been able to solve them and I show the class that I don't have it...yet.
For me, the best POWS are the ones that come to partial solutions and are unfinished. Then students have something to think about and revisit over time as they learn more mathematics.
Do your students present POWs in class? And how do you maintain a focus on the process and not the solution?
It really depends on the grade level I’m working with. With my 4th graders online, students first do the work on their own and share their attempts in breakout rooms. As a group, they try to convince one another which solution makes most sense and come to a consensus on what they will present to the class.
In a traditional classroom, I push students to present halfway through the week and emphasize the incompleteness. I tell them to listen to understand what someone else is trying to help further their own thinking. At the end of the week I get 2-3 students present, but I don't intentionally sequence it, I just ask for volunteers. That works if you have an established community in the classroom where students feel comfortable presenting.

When first implementing POWs, I think it's a good idea to sequence your presentations. The first can be a student who has used some type of diagram to visualize the POW. Then the second presenter can show multiple attempts that they used a process of elimination to determine what does not work.
There are times when no one in the class gets a solution. It's really hard but I don't spill the beans on the solution, because I don’t want to take away from the ‘a-ha moment’ for students.
You also mentioned scaffolding POWs, how does this work?
Usually I will set up checkpoints over the week to see where each student is in their process. The first checkpoint is the problem statement which summarizes what it is they need to solve. Then I’ll check the students' process and I consider this the most important checkpoint. This could be in the last 10 minutes of class or as a quick exit ticket. I’ll let students check in with one another and explain their current ideas, and I’ll chit-chat with students who need a little push or support. Sometimes students solve the POW quickly and I’ll give them an extension to work on, or I’ll connect two students with the same strategy who have different answers. Getting the students to help one another makes it easier for me but it also helps students practice explaining their thinking. I really believe that if you can convince a skeptic of your solution then you probably have a strong case that you are right!
Can POWs be used as a one-off activity or do teachers need to create a regular schedule for using POWs?
I think POWs can be started any time. Halfway through my course with my fourth graders, I started using POWs because I had a POW in mind that would work perfectly for our lesson on systematic lists.
In the regular school year, I use POWs as a regular routine so it helped me to introduce each component clearly and to revisit expectations. You can train students on the POW expectations slowly over time, and you can work on writing problem statements first, then move to teaching how to use diagrams to show their thinking. I normally do 5 POWs per school year or 1 per unit. This gives students enough time to process information between POWs and each time I can build a little bit more into the expectations for the final product. By the last POW of the year, I have my students exchange POWs with a classmate and they provide one another 5 pieces of feedback. It’s great because students get to practice critiquing the reasoning of someone else.

POWs work for me because they work for my students. If you want to try POWs, I recommend to start slowly and the more confident you feel you can assign more. It does take a lot of time to read and grade POWs because students are really explaining their thinking and showing off what they know.
Many teachers feel too busy addressing standards to have time for rich problem solving activities. What would you say to that?
The first thing is, if you feel busy and overwhelmed, your students probably also feel busy and overwhelmed! If you are feeling this way, giving students a break from new content is good for everyone in the long run. It’s ok to pause on the standards, you're building math thinking through POWs that will help students in math.
If you have goals for students to become better writers or presenters, POWs can help with those goals. You can even use POWs related to the content you teach in your class if you feel you can't slow down from your pacing calendar. After 7+ years, I’ve seen the long term benefits of POWS with students at all grade levels and in online and international teaching settings. POWs really benefit all learners around the world.
Where can teachers find POW-worthy problems?
I get my POWs from my curriculum, Interactive Math Program or IMP. There are lots of POWs and rich problems in the book Crossing the River With Dogs. In a traditional textbook you can probably find POW type problems crammed at the end of a unit. They will have good open-ended questions that you can be tweaked and reformatted as a POW. If you plan to tweak an existing problem, I suggest to check the math yourself to make sure you don’t create any issues! I also think a lot of the SBAC released questions are great questions to modify and turn into POWs.
So teachers should work the math before assigning a POW?
Yes! You need to try it yourself! When you do POWs on your own it puts you in the student perspective. I realize how much I am expecting students to do, how much time it will take them, and what support they might need. From my experience of teaching different age groups and in different countries, you may also want to think about modifying a POW to be culturally relevant for your students.
Do you use the same POWs with your high school students as your 4th graders?
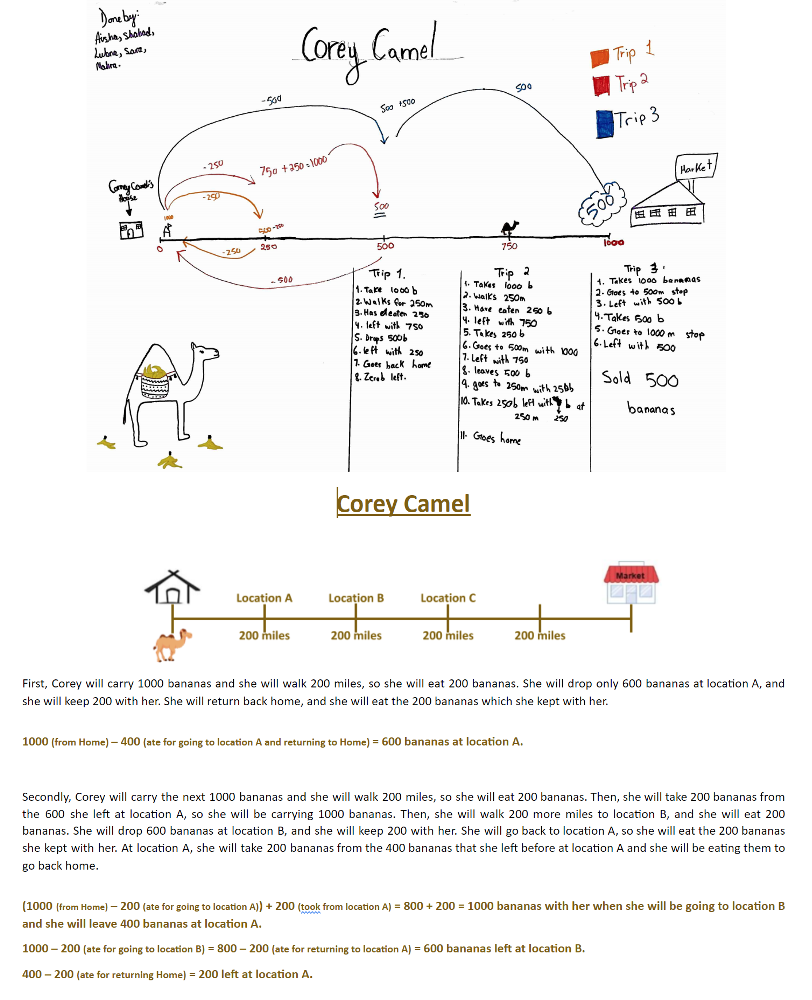
Yep. One of my favorite examples is the Corey Camel POW, it’s the most popular POW with all my students. The 4th graders solve it with models and number lines because those are the tools they know. Middle schoolers like to use tables, and my high school students write novels about Corey Camel with more elaborate diagrams embedded. It’s cool to see how some POWs are done across grade levels.
Another one that has been popular across grade levels is the Broken Eggs POW, the elementary students use an elimination method to solve because that’s what they are learning about. The middle schoolers used tables to look for a pattern, and my high school students solved them with manipulatives. During COVID, students used whatever manipulatives they had at home. One student covered their whole bed in pennies to solve the POW and they had to do it twice because they forgot to count the pennies the first time!
In class students like to work out POWs on the white board. They will take a picture of what they figured out during class and embed the pictures in their write up. It’s a great way to practice organization.

How do you grade or assess POWs?
My first piece of advice is to overlook any spelling and grammar errors in students’ work- don’t be tempted to grade writing like an English teacher!
I grade POWs holistically, sometimes I use a rubric. For me, it is important to be clear about what the expectations are and communicate it to students. I tell them that the process is the most important part. I set up three criteria: diagrams, multiple attempts, and final thoughts on the problem, that’s what I’m looking for. If I have to guess what you're thinking then you're still “practicing the skill” and not mastering.
For kids that don’t see themselves as math students but they like writing, they get a sense of pride in math class through POWs. Kids who are struggling in math are often very proud of their POW even if they aren't right about the solution. Students get a choice on how to display their write-up, and I tell students a POW is not a test! I’m looking to see how they are thinking like a mathematician. I want students to conjecture and use their own math authority to see what makes sense.
I put students back as the decision maker and it reminds them that the teacher is not the source of correctness. When I first started using POWs, that was the hardest thing to unlearn. In class students always looked at me to have the “final say” on what is right or wrong. It takes a lot of time for kids to own the authority, but now kids will come up to me and say, “I know you're not going to tell me if I'm right or wrong, but I'm going to tell you my thinking.” Or a group will say, “You're not going to tell us if it's right or wrong, you're just going to ask us another question.”
Any parting wisdom for our fellow teachers?
Be authentic with your students. We are teachers, but there is so much more to us! You bring into the classroom your beliefs and ideals and so will your students. If you can get kids to see you are a person and you care, it helps them also want to do well in class. There are so many amazing things other teachers do, adapt it to work with your students. Don't force anything! Make it your own, and make it work with your kids and your style.





.png)



