Support Productive Struggle in Learning Mathematics

Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships. 

• Principles to Action, NCTM 2014, p 48

‍

One of the many amazing things about having grandbabies is watching them persevere! During the holidays, I got to observe my toddler grandchildren trying and trying and trying to climb, hop (like a bunny), build, and communicate. During our time together a few months ago, my 4-month-old grandson devoted most of his waking energy to figuring out how to roll over - even though he didn’t know what that was or what would happen when he succeeded! We human beings are born with a beautiful, amazing drive to learn and persevere! 

‍

When my colleagues and I visit classrooms and ask students for feedback about Magma, the most common thing we hear is that they like Magma Math because “I can try as many times as I want and it never makes me stop.” That drive to succeed persists! 

‍

How can we nurture that drive in math classrooms?

Supporting productive struggle in learning mathematics is closely tied to the first Standard for Mathematical Practice: Make sense of problems and persevere in solving them. In some ways, it seems like the grandparent of ALL the standards: with persistence through struggle, anything is possible! 

‍

Supporting productive struggle is a delicate balancing act. We want to provide the right opportunities and supports. The opportunities need to be rigorous enough to be engaging and challenging but not overwhelmingly so. The supports need to be scaffolded enough to provide access but not so much that they impede students or remove all the challenges in a task. Thinking about supporting a toddler as they learn to climb a jungle gym, we want to be there and make sure they aren’t putting themselves at risk of harm, but we don’t want to hover, swoop in, and rescue after little setbacks, or make a big deal about falls and mishaps, and we certainly don’t want to do the climbing for them! 

‍

Productive struggle can be something that students and their parents struggle with! It is something of a new and, for some, off-putting idea in math. I think this is partly because in our culture, we tend to think that if we find math to be hard, we must not be smart in it, rather than thinking that math is a challenge that is hard sometimes but that we can overcome. So, part of supporting productive struggle is intentionally teaching our communities about it. 

‍

This table from NCTM’s Principles to Actions can help us think about supporting Productive Struggle with Magma Math.

Anticipating: Before we ask students to engage in math tasks, we can take the time to solve them in Magma - This is a chance to anticipate barriers our students might encounter and think about what scaffolds we might offer. If we think about this ahead of time, we are more likely to have some helpful questions and prompts ready to go that aren’t “too” helpful. This is also a chance to remember the 5 Practices for facilitating productive discourse. As we solve the problems, we can also anticipate the various solution paths our students might use and the mathematical connections we want to be sure to highlight. 

‍

Time: When I give students an assignment to work on during class time in Magma, I like to structure it so everyone will have time to get to the problems that are at the heart of the lesson, while also creating an on-ramp to get students warmed up, and providing enough problems to keep everyone meaningfully engaged. One way I have found to do this borrows from Dr. Peter Liljedahl’s way of labeling problems as mild, medium, & spicy. Let’s say I’ve created a 12-problem assignment. I start off by telling students that the first 4 problems are mild, the next 4 are medium, and the last 4 are spicy. I tell them they can start anywhere they want and that by a certain time (say in 15 min), I would like everyone to have tried number 5 (one of the medium problems that I think will lead to a deeper conversation.) As students are working, I monitor the heat map, watching for progress, maybe gently nudging a few students to get to #5 in time. Then, when the time is right, we pause working in Magma and have a conversation about the problem, which leads to…

‍

Embracing confusion & errors: In our discussion of the problem I’ve selected (or that the students are struggling with, or one the kids are interested in), we embrace the errors! I’ve been in several classes with this quote from Dr. Jo Boaler posted prominently:

‍

Mistakes are to be EXPECTED, INSPECTED, RESPECTED, and CORRECTED!

‍

When students share their errors, it is a gift to the rest of the class. I always thank them and remind students that mistakes are when we learn! 

‍

One wonderful way to learn from mistakes is to use the My Favorite KNow routine. In this routine, the teacher selects a sample of student work from Magma or creates one with multiple steps that the student has worked correctly and one or two errors. This is a great opportunity to select common errors you see in your students’ work. For example, here is an example from early algebra and geometry. 

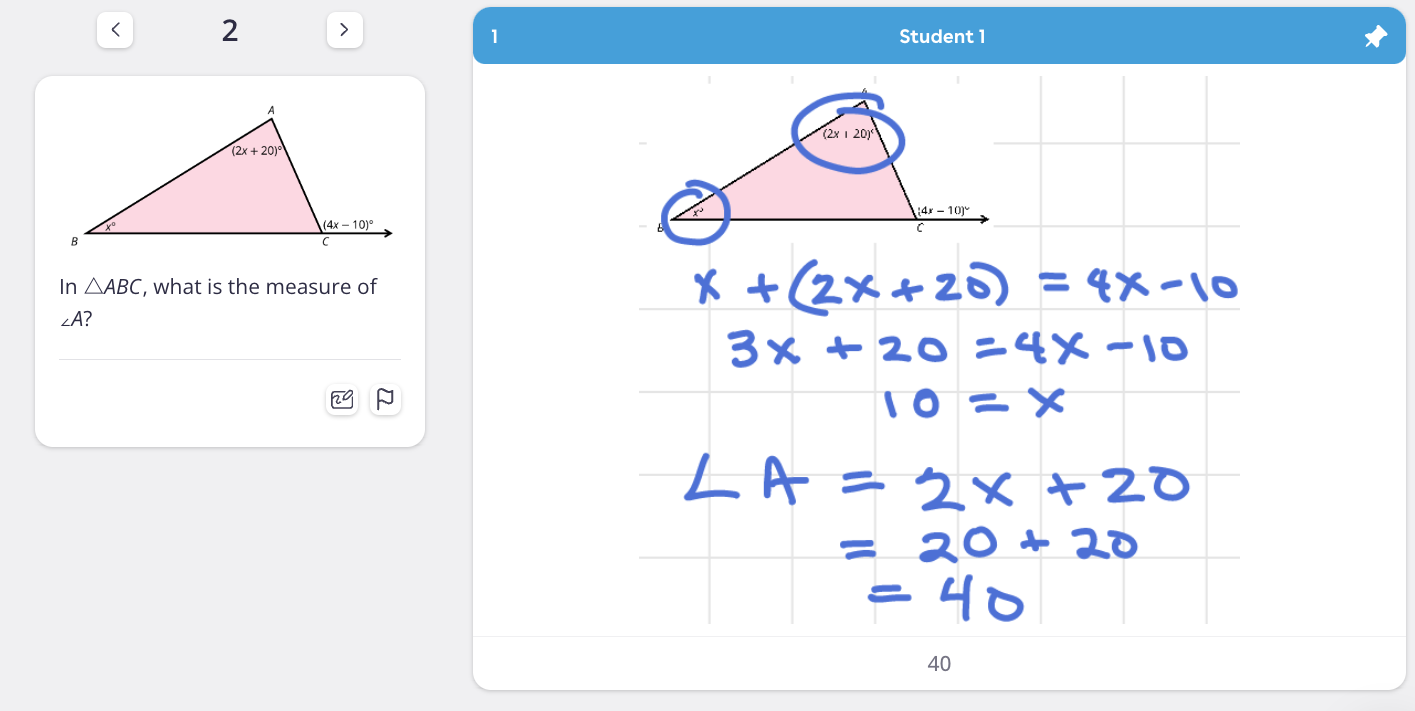
First, we ask students to consider the student's work and look for all the correct things about the problem. I usually have them do this in pairs and encourage them to NOT pivot to finding or naming any errors until I give the signal. Then, we share all of the correct mathematics as a whole class. Only when we’ve got as many correct things named as we can do we focus our attention on locating errors. I ask students how they would respectfully give feedback to their classmate on any potential errors.

‍

Praising students for their efforts & perseverance: Magma enables us to look at and display the record of all the work that a student does as they engage with a problem. This is a wonderful improvement to the days of erasing whole pages of work and/or tossing them in the garbage! When we see that students have made multiple attempts on a problem, we can support them in persevering. One important shift that can occur for students is to realize that rather than delete everything when they make an error, they can examine their work - the same way we do in the My Favorite KNow routine - with an eye to what is correct? And where might I have an error? 

‍

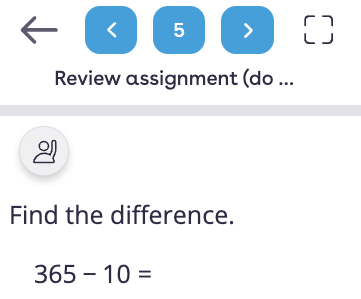
Here is an example of an error that a student made in response to the problem. 

‍

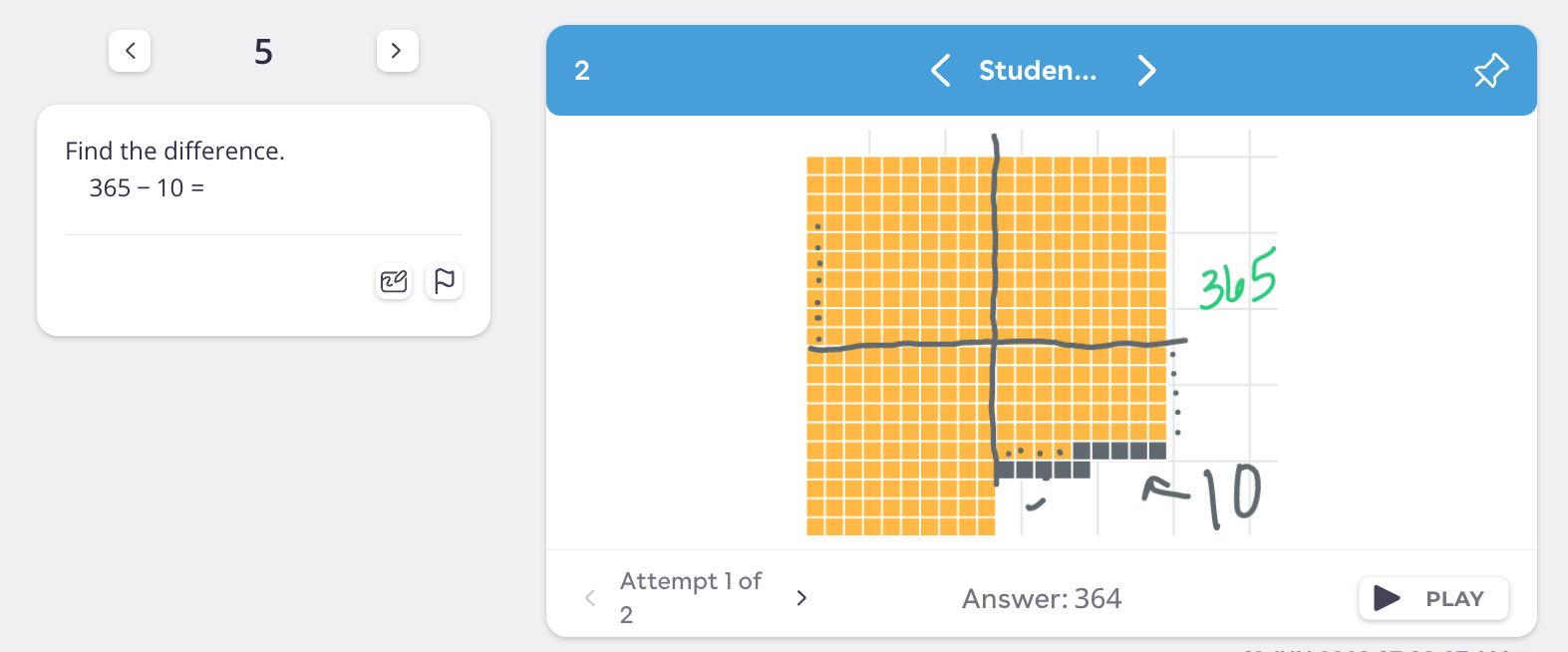
In their first draft, the student said the answer was 364.

‍

‍

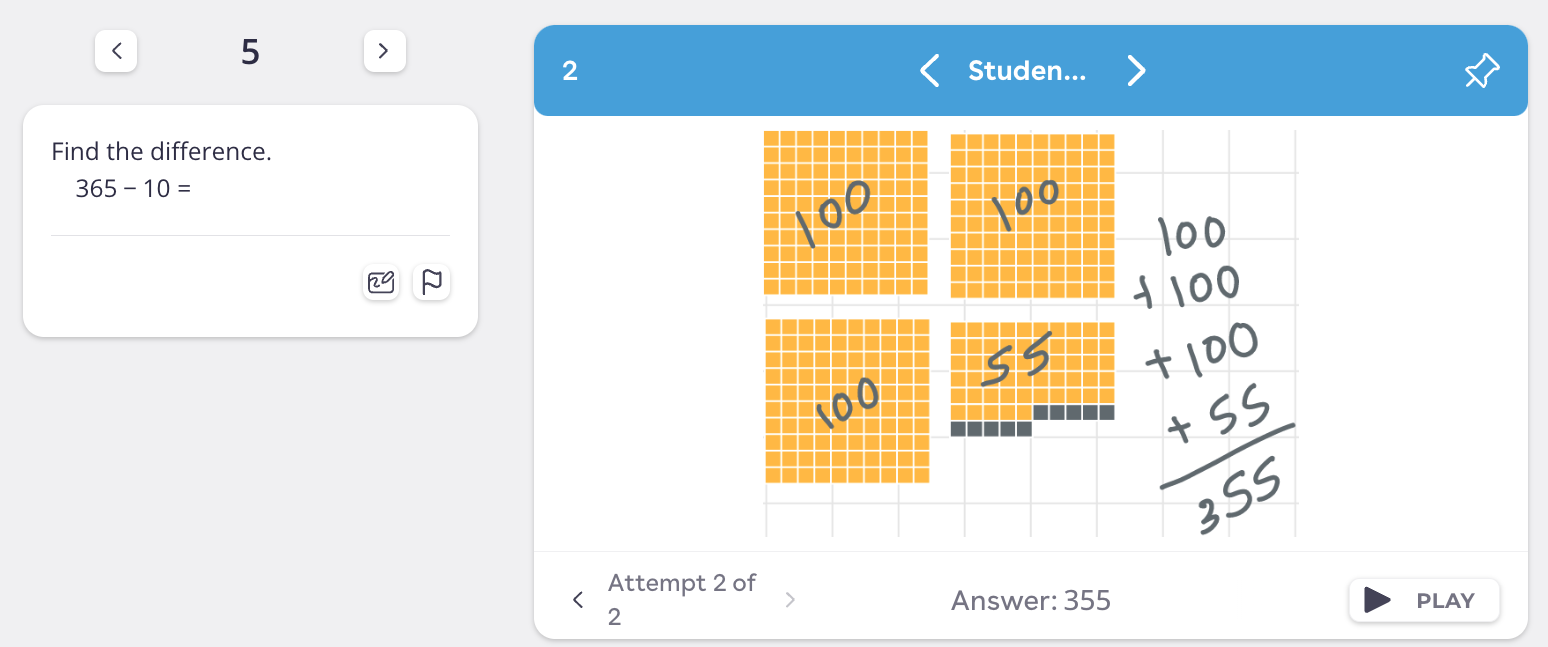
After getting feedback that the answer wasn’t correct, they then separated the tiles, perhaps realizing that they had overlapped the 100 tiles, and corrected their error.

‍

The student’s role: Students have a role to play in productive struggle. As we anticipate, support, and encourage our students, they may need coaching on how to struggle! (Their families may need some support, too!) Learning how to ask questions that are targeted, how to keep on trying, and how to help each other without giving away spoilers. This is achievable in a classroom where we’ve built a culture of learning together and even more so when we can easily share and build on student thinking.

‍